题目内容
1.设函数f(x)是定义在R上的偶函数,且f(1+x)=f(1-x)对任意的x∈R恒成立,且当x∈[0,1]时,f(x)=x2.(1)求证:f(x)是以2为周期的函数(不需要证明2是f(x)的最小正周期);
(2)对于整数k,当x∈[2k-1,2k+1]时,求函数f(x)的解析式;
(3)对于整数k,记Mk={a|f(x)=ax在x∈[2k-1,2x+1]有两个不等的实数根},求集合M2015.
分析 (1)因为f(x+2)=f[(x+1)+1]=-f(x+1)=-[-f(x)]=f(x)可得结论.
(2)先求出x∈[-1,1]时,f(x)=x2,设x∈[2k-1,2k+1],则x-2k∈[-1,1],根据f(x)是以2为周期的函数,即f(x-2k)=f(x)可求解.
(3)将方程f(x)=ax转化为二次函数,利用二次函数根的分布求a的取值集合.
解答 解:(1)因为f(x+2)=f[(x+1)+1]=-f(x+1)=-[-f(x)]=f(x)
所以:f(x)是以2为周期的函数;
(2)∵当x∈[0,1]时,f(x)=x2,函数f(x)是定义在R上的偶函数
∴当x∈[-1,0]时,f(x)=x2,
∴x∈[-1,1]时,f(x)=x2,
∵f(x)是以2为周期的函数,即f(x-2k)=f(x),k∈Z
设x∈[2k-1,2k+1],则x-2k∈[-1,1],
∴f(x-2k)=(x-2k)2,
即f(x)=(x-2k)2,x∈[2k-1,2k+1](k∈Z),
(3)当k∈N*,且x∈Ik 时,方程f(x)=ax化简为x2-(4k+a)x+k2=0,
设g(x)=x2-(4k+a)x+k2,使方程f(x)=ax在Ik上有两个不相等的实数根,
则$\left\{\begin{array}{l}{△=a(a+8k)>0}\\{2k-1<\frac{k+a}{2}≤2k+1}\\{g(2k-1)=1-2ak+a>0}\\{g(2k+1)=1-2ak-a≥0}\end{array}\right.$,
解得0<a≤$\frac{1}{2k+1}$,
当k=2015时,
∴集合M2015=(0,$\frac{1}{4031}$]
点评 本题主要考查函数周期性的应用,以及二次方程根的分布问题,考查学生的转化能力,综合性较强,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 540 | B. | -162 | C. | 162 | D. | -540 |
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 6吨 | 0.9万元 | 0.3万元 |
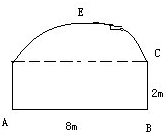 某工程设计一条单行隧道,其横截面如图所示,下部ABCD为长8米高2米的矩形,上部$\widehat{CED}$是圆弧的一部分,欲使宽6米高3米的大型货车刚好能通过,求拱顶E距离路面AB至少需几米?
某工程设计一条单行隧道,其横截面如图所示,下部ABCD为长8米高2米的矩形,上部$\widehat{CED}$是圆弧的一部分,欲使宽6米高3米的大型货车刚好能通过,求拱顶E距离路面AB至少需几米?