题目内容
20.函数f(x)=2x3-6x+11的单调递减区间为(-1,1).分析 先求出函数的导数,通过解导函数小于0,从而求出函数的递减区间.
解答 解:f(x)=2x3-6x+11,f′(x)=6x2-6,
令f′(x)<0,解得:-1<x<1,
故答案为:(-1,1);
点评 本题考察了函数的单调性,导数的应用,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.${(3\sqrt{x}-\frac{1}{{\sqrt{x}}})^6}$的展开式的常数项为( )
| A. | 540 | B. | -162 | C. | 162 | D. | -540 |
8.若|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{2}$,($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=0,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 135° |
9.某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜和韭菜的产量、成本和价格如表所示:
为使一年的种植总利润(总利润=总销售收入-总种植成本)最大,那么黄瓜的面积是30亩.
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 6吨 | 0.9万元 | 0.3万元 |
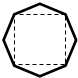 某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成,则该八边形的面积的最大值为$2\sqrt{2}+2$.
某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成,则该八边形的面积的最大值为$2\sqrt{2}+2$. 某工程设计一条单行隧道,其横截面如图所示,下部ABCD为长8米高2米的矩形,上部$\widehat{CED}$是圆弧的一部分,欲使宽6米高3米的大型货车刚好能通过,求拱顶E距离路面AB至少需几米?
某工程设计一条单行隧道,其横截面如图所示,下部ABCD为长8米高2米的矩形,上部$\widehat{CED}$是圆弧的一部分,欲使宽6米高3米的大型货车刚好能通过,求拱顶E距离路面AB至少需几米?