题目内容
7.若点O是△ABC所在平面内的一点,且满足|$\overrightarrow{OB}$-$\overrightarrow{OC}$|=|$\overrightarrow{OB}$+$\overrightarrow{OC}$-2$\overrightarrow{OA}$|,则△ABC的形状为直角三角形.分析 由向量的减法法则,将题中等式化简得$|\overrightarrow{CB}|=|\overrightarrow{AB}+\overrightarrow{AC}|$,进而得到$|\overrightarrow{AB}-\overrightarrow{AC}|=|\overrightarrow{AB}+\overrightarrow{AC}|$,由此可得以AB、AC为邻边的平行四边形为矩形,得到△ABC是直角三角形.
解答 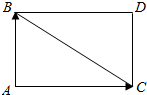 解:∵$\overrightarrow{CB}=\overrightarrow{OB}-\overrightarrow{OC}$,$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$,$\overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA}$
解:∵$\overrightarrow{CB}=\overrightarrow{OB}-\overrightarrow{OC}$,$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$,$\overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA}$
∴$\overrightarrow{|OB}-\overrightarrow{OC}|=|\overrightarrow{OB}+\overrightarrow{OC}-2\overrightarrow{OA}|$,即|$\overrightarrow{CB}$|=$|\overrightarrow{AB}+\overrightarrow{AC}|$
∵$\overrightarrow{CB}=\overrightarrow{AB}-\overrightarrow{AC}$,∴$|\overrightarrow{AB}-\overrightarrow{AC}|=|\overrightarrow{AB}+\overrightarrow{AC}|$,
由此可得以AB、AC为邻边的平行四边形为矩形,
∴∠BAC=90°,得△ABC的形状是直角三角形.
故答案为:直角三角形.
点评 本题给出向量等式,判断三角形ABC的形状,着重考查了平面向量的加法、减法法则和三角形的形状判断等知识,属于中档题.

 53天天练系列答案
53天天练系列答案
| A. | 9 | B. | 11 | C. | 55 | D. | 66 |
| A. | 一定不在一、二象限 | B. | 一定不在二、三象限 | ||
| C. | 一定不在三、四象限 | D. | 一定不在二、三、四象限 |