题目内容
4.在△ABC中,若b=1,$c=\sqrt{3}$,B=30°,则a=( )| A. | 2 | B. | 1 | C. | 1或2 | D. | 2或$\sqrt{3}$ |
分析 由正弦定理可求sinC=$\frac{csinB}{b}$=$\frac{\sqrt{3}}{2}$,结合范围0<C<180°可得C,A的值,由正弦定理即可求得a的值.
解答 解:∵b=1,$c=\sqrt{3}$,B=30°,
∴由正弦定理可得:sinC=$\frac{csinB}{b}$=$\frac{\sqrt{3}×sin30°}{1}$=$\frac{\sqrt{3}}{2}$.
∴由0<C<180°可得:C=60°或120°,从而可解得:A=π-B-C=90°或30°,
∴由正弦定理可得:a=$\frac{bsinA}{sinB}$=$\frac{1×sinA}{sin30°}$=2或1.
故选:C.
点评 本题主要考查了正弦定理,三角形内角和定理等知识的应用,求角C时注意不要漏解,属于基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
19.执行如图所示的程序框图,则输出的结果是( )
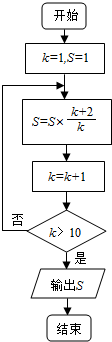

| A. | 9 | B. | 11 | C. | 55 | D. | 66 |
9.某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜和韭菜的产量、成本和价格如表所示:
为使一年的种植总利润(总利润=总销售收入-总种植成本)最大,那么黄瓜的面积是30亩.
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 6吨 | 0.9万元 | 0.3万元 |
14.函数f(x)的定义域为R,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式exf(x)>ex+1,的解集是( )
| A. | {x|x>0} | B. | {x|x<0} | C. | {x|x<-1或x>1} | D. | {x|-1<x<1 } |