题目内容
10.已知函数f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$.(1)求函数f(x)的零点,并求反函数f-1(x);
(2)设g(x)=2log2$\frac{1+x}{k}$,若不等式f-1(x)≤g(x)在区间[$\frac{1}{2}$,$\frac{2}{3}$]上恒成立,求实数k的范围.
分析 (1)由函数f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$=0,由$\left\{\begin{array}{l}{{2}^{x}-1=0}\\{{2}^{x}+1≠0}\end{array}\right.$,解得x即可得出.由y=$\frac{{2}^{x}-1}{{2}^{x}+1}$,解得x=$lo{g}_{2}\frac{1+y}{1-y}$,把x与y互换,即可得出反函数.
(2)k>0,由不等式f-1(x)≤g(x)得到k2≤(1-x)(1+x)=1-x2,再利用二次函数的单调性即可得出.
解答 解:(1)由函数f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$=0,
∴$\left\{\begin{array}{l}{{2}^{x}-1=0}\\{{2}^{x}+1≠0}\end{array}\right.$,解得x=0.
∴函数f(x)的零点是x=0.
由y=$\frac{{2}^{x}-1}{{2}^{x}+1}$,解得${2}^{x}=\frac{1+y}{1-y}$,x=$lo{g}_{2}\frac{1+y}{1-y}$,
把x与y互换,可得f-1(x)=$lo{g}_{2}\frac{1+x}{1-x}$,x∈(-1,1).
(2)∵k>0,
∴$lo{g}_{2}\frac{1+x}{1-x}$≤$2lo{g}_{2}\frac{1+x}{k}$=$lo{g}_{2}(\frac{1+x}{k})^{2}$,
得到k2≤(1-x)(1+x)=1-x2,
∵x∈[$\frac{1}{2}$,$\frac{2}{3}$],
当$x=\frac{2}{3}$时,右边最小值为$\frac{5}{9}$,
解得$0<k≤\frac{\sqrt{5}}{3}$.
∴实数k的范围是$(0,\frac{\sqrt{5}}{3}]$.
点评 本题考查了反函数的求法、二次函数的单调性、指数函数与对数函数的性质,考查了推理能力与计算能力,属于中档题.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案| A. | $\frac{π}{4}$ | B. | $\frac{3π}{8}$ | C. | $\frac{π}{2}$ | D. | π |
 如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )
如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |

| A. | 16+8$\sqrt{3}$ | B. | 16+4$\sqrt{3}$ | C. | 48+8$\sqrt{3}$ | D. | 48+4$\sqrt{3}$ |
| A. | 11 | B. | 66 | C. | 76 | D. | 134 |
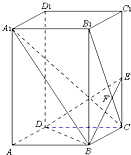 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.