题目内容
1. 如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )
如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
分析 通过联立渐近线y=$\frac{b}{a}$x与直线PF的方程,可得P($\frac{{a}^{2}}{c}$,$\frac{ab}{c}$),利用中点坐标公式可得Q(2$\frac{{a}^{2}}{c}$-c,2$\frac{ab}{c}$),将点Q代入渐近线y=-$\frac{b}{a}$x,计算即得结论.
解答 解:设F(c,0),相应的渐近线:y=$\frac{b}{a}$x,
则直线PF的斜率为-$\frac{a}{b}$,其方程为:y=-$\frac{a}{b}$(x-c),
设P(t,$\frac{b}{a}$t),代入直线PF的方程,
得:$\frac{b}{a}$t=-$\frac{a}{b}$(t-c),解得:t=$\frac{{a}^{2}}{c}$,即P($\frac{{a}^{2}}{c}$,$\frac{ab}{c}$),
∵|PF|=|PQ|,即点P为线段FQ的中点,
∴Q(2$\frac{{a}^{2}}{c}$-c,2$\frac{ab}{c}$),
∵点Q在渐近线y=-$\frac{b}{a}$x上,
∴2$\frac{ab}{c}$=-$\frac{b}{a}$(2$\frac{{a}^{2}}{c}$-c),
化简得:$\frac{c}{a}$=2,即离心率为2,
故选:C.
点评 本题主要考查双曲线的几何性质,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
12.已知直线y=-x+1与圆C:x2+y2-4x+3=0相较于A,B两点,则|AB|的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
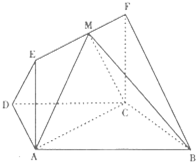 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.