Question

2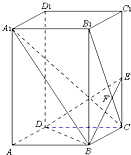．如图，已知正四棱柱ABCD-A₁B₁C₁D₁中，底面边长AB=2，侧棱BB₁的长为4，过点B作B₁C的垂线交侧棱CC₁于点E，交B₁C于点F．
（1）求证：A₁C⊥平面BDE；
（2）求三棱锥C-BDE的体积．

Answer 1

分析 （1）先证明：BD⊥A₁C，BE⊥A₁C，再证明A₁C⊥平面BDE；
（2）利用V_C-BDE=V_E-BDC，求三棱锥C-BDE的体积．

解答 （1）证明：因为BD⊥AC，BD⊥AA₁，AC∩AA₁=A，
所以BD⊥平面A₁AC，
所以BD⊥A₁C；（3分）
又因为BE⊥B₁C，BE⊥A₁B₁，B₁C∩A₁B₁=B₁，
所以BE⊥平面A₁B₁C，
所以BE⊥A₁C；
因为BD∩BE=B
所以A₁C⊥平面BDE．（6分）
（2）解：由题意CE=1，（8分）
所以V_C-BDE=V_E-BDC=$\frac{1}{3}×1×\frac{1}{2}×2×2$=$\frac{2}{3}$（14分）

点评 本题考查线面垂直，考查三棱锥C-BDE的体积，考查学生分析解决问题的能力，属于中档题．