题目内容
5.函数f(x)是定义在实数集R上的不恒为零的偶函数,f(-1)=1,且对任意实数x都有xf(x+1)=(x+1)f(x),则f(0)+f(1)+f(2)+…+f(2015)的值是2031120.分析 从xf(x+1)=(1+x)f(x)结构来看,要用递推的方法,先用赋值法求得.
解答 解:∵xf(x+1)=(x+1)f(x),
∴当x=0时f(0)=0,
∵f(x)是定义在实数集R上的不恒为零的偶函数且f(-1)=1,
∴f(1)=f(-1)=1.
∵xf(x+1)=(x+1)f(x),
∴$f(x+1)=\frac{x+1}{x}f(x)$
当x=1时f(2)=2,
当x=2时f(3)=3,
当x=3时f(4)=4,
…
当x=2014时f(2015)=2015
则f(0)+f(1)+f(2)+…+f(2015)=0+1+2+3+4+5+…+2015=2031120
∴故答案为:2031120
点评 本题主要考查利用函数的主条件用递推的方法求函数值,这类问题关键是将条件和结论有机地结合起来,作适当变形,把握递推的规律.

练习册系列答案
相关题目
15.若集合M={y|y=sinx},N={x|x2-4≤0},则M∩N=( )
| A. | Φ | B. | [-2,2] | C. | [-1,1] | D. | {-1,1} |
12.复数${({\frac{1-i}{{\sqrt{2}}}})^{2015}}$计算的结果是( )
| A. | -1 | B. | -i | C. | $\frac{1+i}{{\sqrt{2}}}$ | D. | $\frac{-1+i}{{\sqrt{2}}}$ |
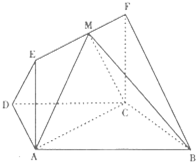 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.