题目内容
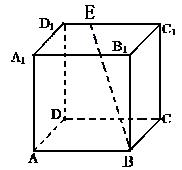
(本小题满分10分)如图,在棱长为ɑ的正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
(1)求证:平面A B1D1∥平面EFG;
(2)求证:平面AA1C⊥面EFG .
(1)求证:平面A B1D1∥平面EFG;
(2)求证:平面AA1C⊥面EFG .

略
解:(1)在正方体ABCD-A1B1C1D1中连接BD,
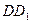 ∥
∥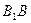 ,
,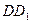 =
=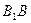 ,
,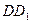
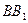 为平行四边形 ∴
为平行四边形 ∴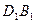 ∥
∥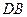
∵E,F分别为BC,CD的中点
∴EF∥BD ∴EF∥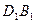
∵EF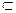 平面GEF,
平面GEF,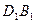
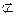 平面GEF
平面GEF
∴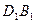 ∥平面GEF
∥平面GEF
同理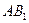 ∥平面GEF
∥平面GEF
∵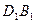
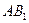 =
=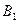
∴平面A B1D1∥平面EFG ……………5分
(2)在正方体ABCD-A1B1C1D1 ∴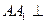 平面ABCD
平面ABCD
∵EF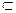 平面ABCD ∴
平面ABCD ∴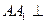 EF
EF
∵ABCD为正方形 ∴AC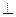 BD
BD
∵EF∥BD ∴AC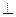 EF 又∵
EF 又∵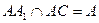
∴EF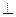 平面AA1C
平面AA1C
∵EF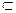 平面EFG ∴平面AA1C⊥面EFG …………….5分
平面EFG ∴平面AA1C⊥面EFG …………….5分
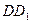 ∥
∥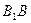 ,
,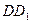 =
=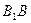 ,
,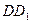
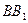 为平行四边形 ∴
为平行四边形 ∴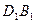 ∥
∥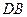
∵E,F分别为BC,CD的中点
∴EF∥BD ∴EF∥
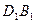
∵EF
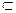 平面GEF,
平面GEF,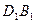
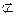 平面GEF
平面GEF∴
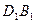 ∥平面GEF
∥平面GEF 同理
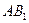 ∥平面GEF
∥平面GEF∵
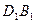
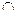
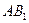 =
=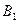
∴平面A B1D1∥平面EFG ……………5分
(2)在正方体ABCD-A1B1C1D1 ∴
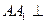 平面ABCD
平面ABCD∵EF
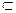 平面ABCD ∴
平面ABCD ∴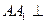 EF
EF ∵ABCD为正方形 ∴AC
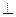 BD
BD∵EF∥BD ∴AC
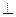 EF 又∵
EF 又∵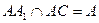
∴EF
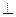 平面AA1C
平面AA1C∵EF
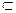 平面EFG ∴平面AA1C⊥面EFG …………….5分
平面EFG ∴平面AA1C⊥面EFG …………….5分
练习册系列答案
相关题目
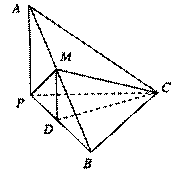
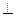 底面ABCD,PA=AB=
底面ABCD,PA=AB=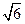 ,点E是棱PB的中点。(1)求直线AD与平面PBC的距离。
,点E是棱PB的中点。(1)求直线AD与平面PBC的距离。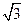 ,求二面角A-EC-D的平面角的余弦值。
,求二面角A-EC-D的平面角的余弦值。
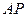 是⊙
是⊙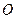 的切线,
的切线, 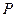 为切点,
为切点,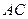 是⊙O的割线,与⊙
是⊙O的割线,与⊙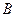 ,
,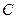 两点,圆心
两点,圆心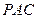 的内部,点
的内部,点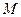 是
是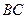 的中点.
的中点.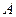 ,
,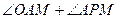 的大小.
的大小.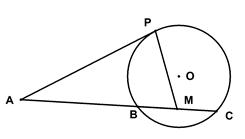
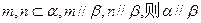 .
. ____.
____.
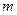 、
、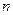 与平面
与平面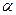 、
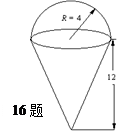
、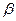 ,有下列四个命题:
,有下列四个命题: 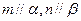 且
且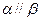 ,则
,则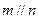 ; ②
; ②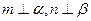 且
且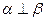 ,则
,则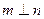 ;
;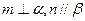 且
且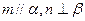 且
且