题目内容
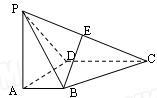
如图四棱锥P-ABCD中,底面ABCD为矩形,PA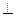 底面ABCD,PA=AB=
底面ABCD,PA=AB=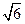 ,点E是棱PB的中点。(1)求直线AD与平面PBC的距离。
,点E是棱PB的中点。(1)求直线AD与平面PBC的距离。
(2)若AD=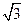 ,求二面角A-EC-D的平面角的余弦值。
,求二面角A-EC-D的平面角的余弦值。
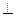 底面ABCD,PA=AB=
底面ABCD,PA=AB=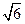 ,点E是棱PB的中点。(1)求直线AD与平面PBC的距离。
,点E是棱PB的中点。(1)求直线AD与平面PBC的距离。(2)若AD=
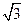 ,求二面角A-EC-D的平面角的余弦值。
,求二面角A-EC-D的平面角的余弦值。见解析
(1)如图(1),在矩形ABCD中,AD∥BC,从而AD∥平面PBC,故直线AD与平面PBC的
距离为点A到平面PBC的距离(2分)。因为PA⊥AB, 由PA=AB知 PAB为等腰直角三角形,又点E是棱PB的中点,故AE⊥PB,又在矩形ABCD中,BC⊥AB,而AB是PB在底面ABCD内和射影,由三垂线定理得BC⊥PB,从而BC⊥PAB(4分)。故BC⊥AE,从而AE⊥平面PBC,故AE的长即为直线AD与平面PBC的距离,在Rt
由PA=AB知 PAB为等腰直角三角形,又点E是棱PB的中点,故AE⊥PB,又在矩形ABCD中,BC⊥AB,而AB是PB在底面ABCD内和射影,由三垂线定理得BC⊥PB,从而BC⊥PAB(4分)。故BC⊥AE,从而AE⊥平面PBC,故AE的长即为直线AD与平面PBC的距离,在Rt PAB中,PA=AB=
PAB中,PA=AB=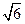 ,所以
,所以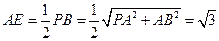 。……………………………………6`
。……………………………………6`
(2)过点D作DF⊥CE,交CE于F,过点F作FG⊥CE,交AC于G,则∠DFG为 所求的二面角的平面角。……………………………………………8`
所求的二面角的平面角。……………………………………………8`
由(1)知BC⊥平面PAB,又AD⊥平面PAB,又AD∥BC,得AD⊥平面PAB,故AD⊥AE,从而DE=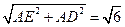 。
。
在Rt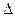 CBE中,
CBE中,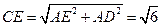 .由CD=
.由CD=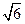 ,知
,知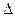 CDE为等边三角形,故F为CE的中点,且
CDE为等边三角形,故F为CE的中点,且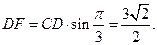
因为AE⊥平面PBC,故AE⊥CE。又FG⊥CE,知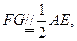 从而
从而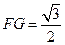 ,且G点为AC的中点,连接DG,则在
,且G点为AC的中点,连接DG,则在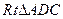 中,
中,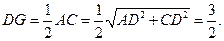 …………………………………………10`
…………………………………………10`
所以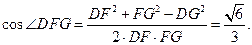
所以二面角A-EC-D的平面角的余弦值为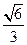 。…………………………12`
。…………………………12`
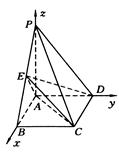 解
解 法2:(1)如图(2),以A为坐标原点,
法2:(1)如图(2),以A为坐标原点,
射线AB、AD、AP分别为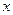 轴、
轴、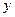 轴、
轴、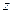 轴
轴
正半轴,建立空间直角坐标系A-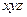 。
。
设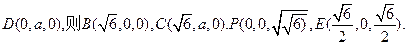 ………2`
………2`
因此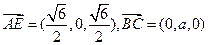 ,
,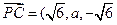 ,
,
则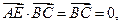
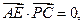 所以AE⊥平面PBC。………4`
所以AE⊥平面PBC。………4`
又由AD∥BC加AD∥平面PBC,故直线AD与平面PBC的距离为点A到平面PBC的距离,即为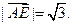 ………6`
………6`
(2)因为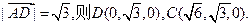
设平面AEC的法向量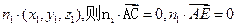
又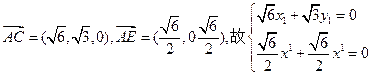
所以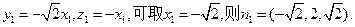 …………8`
…………8`
设平面DEC的法向量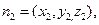
则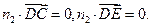
又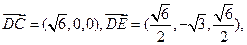 故
故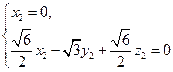
所以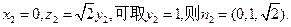 ……………………10`
……………………10`
故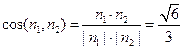 …………12`
…………12`
所以三角形A-EC-D的平面角的余弦值为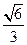 。
。
距离为点A到平面PBC的距离(2分)。因为PA⊥AB,
 由PA=AB知 PAB为等腰直角三角形,又点E是棱PB的中点,故AE⊥PB,又在矩形ABCD中,BC⊥AB,而AB是PB在底面ABCD内和射影,由三垂线定理得BC⊥PB,从而BC⊥PAB(4分)。故BC⊥AE,从而AE⊥平面PBC,故AE的长即为直线AD与平面PBC的距离,在Rt
由PA=AB知 PAB为等腰直角三角形,又点E是棱PB的中点,故AE⊥PB,又在矩形ABCD中,BC⊥AB,而AB是PB在底面ABCD内和射影,由三垂线定理得BC⊥PB,从而BC⊥PAB(4分)。故BC⊥AE,从而AE⊥平面PBC,故AE的长即为直线AD与平面PBC的距离,在Rt PAB中,PA=AB=
PAB中,PA=AB=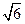 ,所以
,所以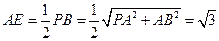 。……………………………………6`
。……………………………………6`(2)过点D作DF⊥CE,交CE于F,过点F作FG⊥CE,交AC于G,则∠DFG为
 所求的二面角的平面角。……………………………………………8`
所求的二面角的平面角。……………………………………………8`由(1)知BC⊥平面PAB,又AD⊥平面PAB,又AD∥BC,得AD⊥平面PAB,故AD⊥AE,从而DE=
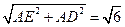 。
。在Rt
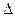 CBE中,
CBE中,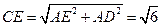 .由CD=
.由CD=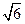 ,知
,知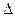 CDE为等边三角形,故F为CE的中点,且
CDE为等边三角形,故F为CE的中点,且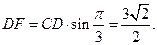
因为AE⊥平面PBC,故AE⊥CE。又FG⊥CE,知
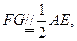 从而
从而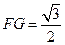 ,且G点为AC的中点,连接DG,则在
,且G点为AC的中点,连接DG,则在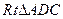 中,
中,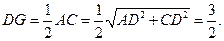 …………………………………………10`
…………………………………………10`所以
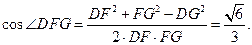
所以二面角A-EC-D的平面角的余弦值为
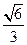 。…………………………12`
。…………………………12` 解
解 法2:(1)如图(2),以A为坐标原点,
法2:(1)如图(2),以A为坐标原点,射线AB、AD、AP分别为
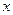 轴、
轴、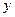 轴、
轴、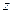 轴
轴正半轴,建立空间直角坐标系A-
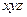 。
。设
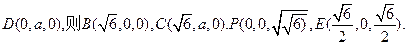 ………2`
………2`因此
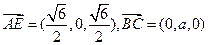 ,
,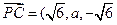 ,
,则
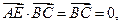
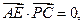 所以AE⊥平面PBC。………4`
所以AE⊥平面PBC。………4`又由AD∥BC加AD∥平面PBC,故直线AD与平面PBC的距离为点A到平面PBC的距离,即为
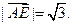 ………6`
………6`(2)因为
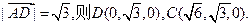
设平面AEC的法向量
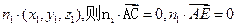
又
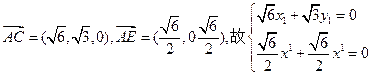
所以
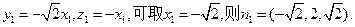 …………8`
…………8`设平面DEC的法向量
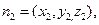
则
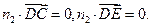
又
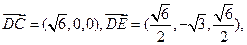 故
故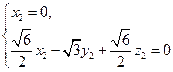
所以
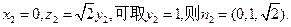 ……………………10`
……………………10`故
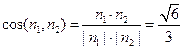 …………12`
…………12`所以三角形A-EC-D的平面角的余弦值为
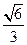 。
。
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目

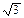 的圆柱,求圆柱的表面积
的圆柱,求圆柱的表面积
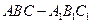 所有棱
所有棱 长都是
长都是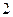 ,
,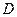 是棱
是棱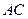 的中点,
的中点,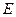 是棱
是棱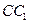 的中点,
的中点,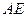 交
交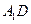 于点
于点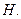
 ;
;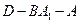 的大小(用反三角函数表示);
的大小(用反三角函数表示);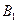 到平面
到平面 的距离.
的距离.
 成角的余弦值;
成角的余弦值;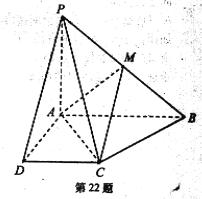
 中,
中,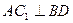 (2)平面
(2)平面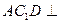 平面
平面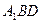
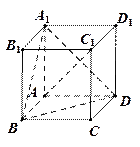
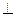 AD,BC
AD,BC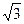 ,则此三棱锥外接球的体积为
,则此三棱锥外接球的体积为 