题目内容
(9分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点.
(1)求直线BE与平面ABCD所成角的正切值;
(2)在侧面PAB内找一点N,使NE⊥面PAC,
并求出N点到AB和AP的距离.
(1)求直线BE与平面ABCD所成角的正切值;
(2)在侧面PAB内找一点N,使NE⊥面PAC,
并求出N点到AB和AP的距离.

(1)直线BE与平面ABCD所成角的正切值 .
.
(2)N点到AB的距离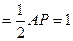 ,N点到AP的距离
,N点到AP的距离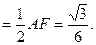
 .
.(2)N点到AB的距离
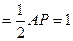 ,N点到AP的距离
,N点到AP的距离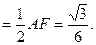
解:方法一、(1)取AD中点F,连接EF、BF,则EF//PA,
由侧棱PA⊥底面ABCD,∴EF⊥底面ABCD,则∠EBF为BE与
平面ABCD所成角
∴在△EBF中,EF=1,BF= ,tan∠EBF=
,tan∠EBF=
即直线BE与平面ABCD所成角的正切值 .
.
(2)在面ABCD内过D作AC的垂线交AB于F,则 .
.
连PF,则在Rt△ADF中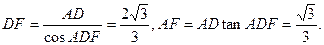
设N为PF的中点,连NE,则NE//DF,
∵DF⊥AC,DF⊥PA,∴DF⊥面PAC,从而NE⊥面PAC.
∴N点到AB的距离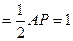 ,N点到AP的距离
,N点到AP的距离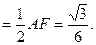
由侧棱PA⊥底面ABCD,∴EF⊥底面ABCD,则∠EBF为BE与
平面ABCD所成角
∴在△EBF中,EF=1,BF=
 ,tan∠EBF=
,tan∠EBF=
即直线BE与平面ABCD所成角的正切值
 .
.(2)在面ABCD内过D作AC的垂线交AB于F,则
 .
.连PF,则在Rt△ADF中
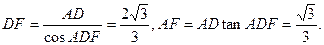
设N为PF的中点,连NE,则NE//DF,
∵DF⊥AC,DF⊥PA,∴DF⊥面PAC,从而NE⊥面PAC.
∴N点到AB的距离
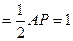 ,N点到AP的距离
,N点到AP的距离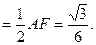

练习册系列答案
相关题目
 .
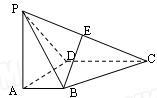
.  中, 底面ABCD是正方形,且
中, 底面ABCD是正方形,且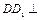 底面
底面 ,
, .
. 与
与 所成角的余弦值;
所成角的余弦值; 中确定一个点
中确定一个点 ,使得
,使得 平面
平面 ;
; 的余弦值.
的余弦值.
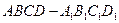 中,以正方体的三条棱所在直线为轴建立空间直角坐标系
中,以正方体的三条棱所在直线为轴建立空间直角坐标系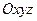 ,
,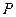 在线段
在线段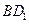 上,且满足
上,且满足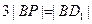 ,试写出点
,试写出点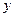 轴的对称点
轴的对称点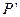 的坐标;
的坐标;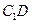 上找一点
上找一点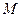 ,使得点
,使得点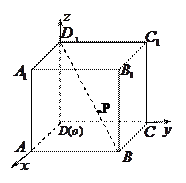
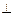 平面PAD;
平面PAD;

 成角的余弦值;
成角的余弦值;
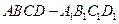 的棱长为
的棱长为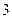 ,点
,点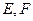 在线段
在线段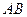 上,点
上,点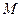 在线段
在线段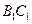 上,点
上,点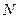 在线段
在线段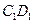 上,且
上,且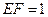 ,
,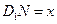 ,
,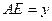 ,
,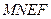 的体积( )
的体积( )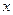 有关,与
有关,与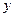 无关
无关