题目内容
选修4-1:几何证明选讲
如图,已知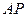 是⊙
是⊙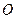 的切线,
的切线, 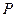 为切点,
为切点,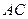 是⊙O的割线,与⊙
是⊙O的割线,与⊙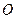 交于
交于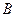 ,
,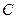 两点,圆心
两点,圆心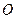 在
在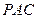 的内部,点
的内部,点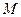 是
是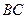 的中点.
的中点.
(1)求证: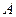 ,
,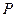 ,
,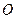 ,
,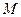 四点共圆;
四点共圆;
(2)求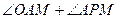 的大小.
的大小.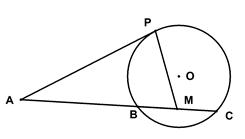
如图,已知
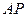 是⊙
是⊙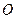 的切线,
的切线, 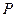 为切点,
为切点,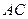 是⊙O的割线,与⊙
是⊙O的割线,与⊙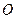 交于
交于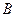 ,
,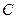 两点,圆心
两点,圆心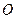 在
在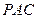 的内部,点
的内部,点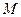 是
是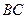 的中点.
的中点.(1)求证:
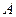 ,
,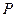 ,
,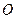 ,
, 四点共圆;
四点共圆;(2)求
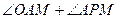 的大小.
的大小.
(1)证明略; (2)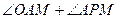 =
=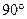
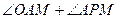 =
=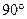
略

练习册系列答案
相关题目
题目内容
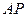 是⊙
是⊙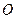 的切线,
的切线, 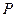 为切点,
为切点,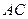 是⊙O的割线,与⊙
是⊙O的割线,与⊙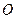 交于
交于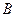 ,
,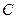 两点,圆心
两点,圆心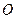 在
在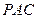 的内部,点
的内部,点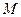 是
是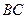 的中点.
的中点.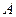 ,
,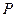 ,
,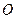 ,
, 四点共圆;
四点共圆;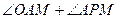 的大小.
的大小.
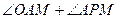 =
=