题目内容
关于直线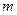 、
、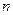 与平面
与平面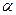 、
、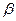 ,有下列四个命题:
,有下列四个命题:
①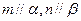 且
且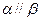 ,则
,则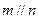 ; ②
; ②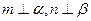 且
且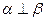 ,则
,则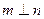 ;
;
③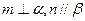 且
且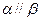 ,则
,则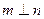 ; ④
; ④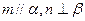 且
且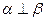 ,则
,则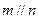 .
.
其中正确命题的个数是( )
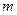 、
、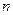 与平面
与平面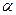 、
、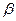 ,有下列四个命题:
,有下列四个命题: ①
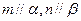 且
且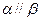 ,则
,则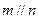 ; ②
; ②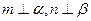 且
且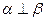 ,则
,则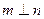 ;
;③
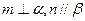 且
且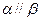 ,则
,则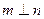 ; ④
; ④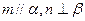 且
且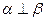 ,则
,则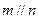 .
.其中正确命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
B
略

练习册系列答案
相关题目
题目内容
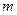 、
、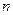 与平面
与平面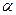 、
、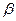 ,有下列四个命题:
,有下列四个命题: 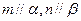 且
且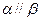 ,则
,则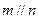 ; ②
; ②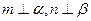 且
且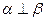 ,则
,则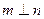 ;
;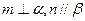 且
且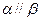 ,则
,则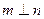 ; ④
; ④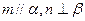 且
且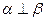 ,则
,则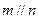 .
.| A.1 | B.2 | C.3 | D.4 |
