��Ŀ����
����Ŀ��ij���ÿ������滮Ҫ��һ����ͣ������ͣ�������������ͼ��ʾ����Բ��AMB������APΪ2���ף�BPΪ4���ף�![]() ��MΪ����Բ������A��B��һ���㣬��
��MΪ����Բ������A��B��һ���㣬��![]() ������ֵΪ
������ֵΪ![]() ƽ�����ף���ͼ��ϵ��
ƽ�����ף���ͼ��ϵ��
![]() �������Բ���ķ��̣�
�������Բ���ķ��̣�
![]() ��Ҫ��������ͣ�����ڳ������˵�ָ��λ��P����NΪ�����㣬��A,BΪ���ڣ�Ҫʹ������ʡ�������̲���Ҫָ��һ���ֽ��ߣ�������ֽ������ڵ����߷��̣�
��Ҫ��������ͣ�����ڳ������˵�ָ��λ��P����NΪ�����㣬��A,BΪ���ڣ�Ҫʹ������ʡ�������̲���Ҫָ��һ���ֽ��ߣ�������ֽ������ڵ����߷��̣�
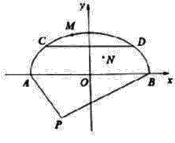
![]() ���ڰ���Բ��ͣ�������Ϸ��������̳������ε�һ��CD��ABƽ�У���
���ڰ���Բ��ͣ�������Ϸ��������̳������ε�һ��CD��ABƽ�У���![]() ���ף���ȷ��t��ֵ��ʹ�̳������������
���ף���ȷ��t��ֵ��ʹ�̳������������
���𰸡�![]()
![]()
![]()
![]()
![]()
��������
��1����ֱ��������PAB�У�����֪��Ϲ��ɶ�����AB������Բ����Ϊ![]() ��a��b��0��������֪��ʽ���a��b������Բ���̿���
��a��b��0��������֪��ʽ���a��b������Բ���̿���
��2������N��P��·����ȣ��ɵ�NA+AP��NB+BP����NA��NB��2��AB����N����A��BΪ�����˫�����ϣ���˫���߷���Ϊ![]() ��m��0��n��0������
��m��0��n��0������![]() �����m��n��ֵ����˫���߷��̿���
�����m��n��ֵ����˫���߷��̿���
��3����CD��2t����D��t��s����s��0������![]() �����s�����̳������Ϊy��2ts��2t
�����s�����̳������Ϊy��2ts��2t![]() ��Ȼ�����û�������ʽ����ֵ��
��Ȼ�����û�������ʽ����ֵ��
![]() ��ֱ��������PAB�У�
��ֱ��������PAB�У�![]() ��
��![]() ��
��
�ɹ��ɶ����ã�![]() ��
��
����Բ����Ϊ![]() ��
��
�������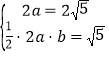 �����
�����![]() ��
��![]() ��
��
![]() ��Բ���ķ���Ϊ
��Բ���ķ���Ϊ![]() ��
��
![]() �ɵ�N��P��·����ȣ�
�ɵ�N��P��·����ȣ�![]() ����
����![]() ��
��
��![]() ��
��![]() ����A��BΪ�����˫�����ϣ�
����A��BΪ�����˫�����ϣ�
��˫���߷���Ϊ![]() ��
��
��![]() �����
�����![]() ��
��![]() ��
��
![]() ˫���߷���Ϊ
˫���߷���Ϊ![]() ��
��
![]() ��
��![]() ����
����![]() ����
����![]() ��
��
![]() ��
��
![]() �̳������Ϊy��2ts��2t
�̳������Ϊy��2ts��2t![]() ��
��
![]() ��
��![]() ��
��
��![]() ��
��
���ҽ���![]() ����
����![]() ʱ��
ʱ��![]() ��������
��������
![]() ��
��![]() ʱ���̳������������Ϊ
ʱ���̳������������Ϊ![]() ƽ�����ף�
ƽ�����ף�

 ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�