题目内容
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润30元,未售出的产品,每盒亏损10元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以![]() (单位:盒,
(单位:盒, ![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量, ![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.
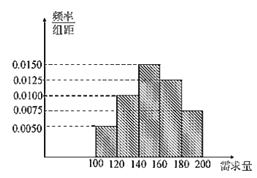
(1)根据直方图估计这个开学季内市场需求量![]() 的平均数;
的平均数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润![]() 不少于4000元的概率.
不少于4000元的概率.
【答案】(1)153;(2) ![]() ;(3)0.7.
;(3)0.7.
【解析】试题分析:(1)根据分布图先算出各频率,然后再计算求出平均数(2)分类讨论当![]() 时及当
时及当![]() 时两种情况,分别写出解析式(3)代入求解结果即可
时两种情况,分别写出解析式(3)代入求解结果即可
解析:(1)需求量为![]() 的频率
的频率![]() ,
,
需求量为![]() 的频率
的频率![]() ,
,
需求量为![]() 的频率
的频率![]() ,
,
需求量为![]() 的频率
的频率![]() ,
,
需求量为![]() 的频率
的频率![]() .
.
则平均数![]() .
.
(2)因为每售出1盒该产品获利润30元,未售出的产品,每盒亏损10元,
所以当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]()
(3)因为利润不少于4000元,解得![]() ,解得
,解得![]() .
.
所以由(1)知利润不少于4000元的概率![]() .
.

【题目】在高中学习过程中,同学们常这样说:“如果你的物理成绩好,那么你的数学学习就不会有什么大问题.”某班针对“高中物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系,如表为该班随机抽取6名学生在一次考试中的物理和数学成绩:
学生编号 学科 | 1 | 2 | 3 | 4 | 5 | 6 |
物理成绩(x) | 75 | 65 | 75 | 65 | 60 | 80 |
数学成绩(y) | 125 | 117 | 110 | 103 | 95 | 110 |
(1)求数学成绩y对物理成绩x的线性回归方程;
(2)该班某同学的物理成绩100分,预测他的数学成绩.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
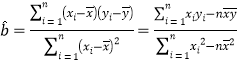 ,
,![]()
参考数据:752+652+752+652+602+802=29700,
75×125+65×117+75×110+65×103+60×95+80×110=46425.
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 |
|
|
|
|
加工的时间 |
|
|
|
|
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(3)试预测加工![]() 个零件需要多少时间?
个零件需要多少时间?
附录:参考公式: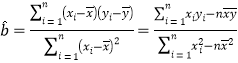 ,
,![]() .
.