题目内容
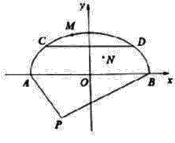
【题目】【2018届四川省成都市第七中学高三上学期模拟】已知椭圆![]() 的一个焦点
的一个焦点![]() ,且过点
,且过点![]() ,右顶点为
,右顶点为![]() ,经过点
,经过点![]() 的动直线
的动直线![]() 与椭圆交于
与椭圆交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 是椭圆
是椭圆![]() 上一点,
上一点, ![]() 的角平分线交
的角平分线交![]() 轴于
轴于![]() ,求
,求![]() 的长;
的长;
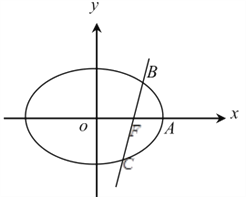
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得点
,使得点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 落在
落在![]() 上?若存在,求出
上?若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在点
;(3)存在点![]() 满足条件.
满足条件.
【解析】试题分析:(1)将点的坐标代入椭圆方程,与c=1联立方程组解得![]() (2)由角平分线定理得
(2)由角平分线定理得![]() ,解得N坐标,再根据两点间距离公式求
,解得N坐标,再根据两点间距离公式求![]() 的长;(3)根据对称得
的长;(3)根据对称得![]() ,设
,设![]() ,利用斜率公式转化得
,利用斜率公式转化得![]() ,代入直线方程化简得
,代入直线方程化简得![]() ,联立直线方程与椭圆方程,利用韦达定理代入化简即得
,联立直线方程与椭圆方程,利用韦达定理代入化简即得![]() 最后根据方程恒成立条件得
最后根据方程恒成立条件得![]()
试题解析:(1)由已知得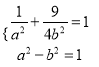 ,解得
,解得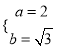 ,
,
∴椭圆方程为![]()
(2)依题可得![]() ,由平面几何角平分线定理得
,由平面几何角平分线定理得
![]() ,即
,即![]() ,得
,得![]()
所以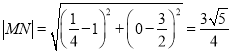
(3)假设在![]() 轴上存在一点
轴上存在一点![]() 满足已知条件,则
满足已知条件,则![]()
即![]()

整理得: ![]() ,∵
,∵![]() 任意,∴
任意,∴![]()
故存在点![]() 满足条件.
满足条件.

 培优三好生系列答案
培优三好生系列答案【题目】在高中学习过程中,同学们常这样说:“如果你的物理成绩好,那么你的数学学习就不会有什么大问题.”某班针对“高中物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系,如表为该班随机抽取6名学生在一次考试中的物理和数学成绩:
学生编号 学科 | 1 | 2 | 3 | 4 | 5 | 6 |
物理成绩(x) | 75 | 65 | 75 | 65 | 60 | 80 |
数学成绩(y) | 125 | 117 | 110 | 103 | 95 | 110 |
(1)求数学成绩y对物理成绩x的线性回归方程;
(2)该班某同学的物理成绩100分,预测他的数学成绩.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
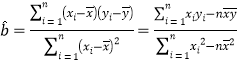 ,
,![]()
参考数据:752+652+752+652+602+802=29700,
75×125+65×117+75×110+65×103+60×95+80×110=46425.
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 |
|
|
|
|
加工的时间 |
|
|
|
|
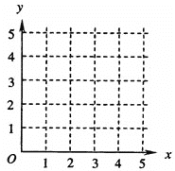
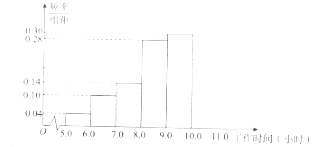
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(3)试预测加工![]() 个零件需要多少时间?
个零件需要多少时间?
附录:参考公式: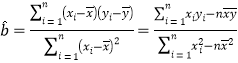 ,
,![]() .
.