题目内容
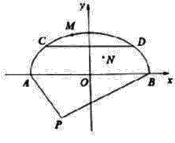
【题目】已知椭圆C中心在原点,焦点在x轴上,左右焦点分别为F1,F2,且|F1F2|=2,点(1,![]() )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的方程;
(2)过F1的直线l与椭圆C相交于A,B两点,且△AF2B的面积为![]() ,求以F2为圆心且与直线l相切的圆的方程.
,求以F2为圆心且与直线l相切的圆的方程.
【答案】(Ⅰ)![]() (Ⅱ)(x﹣1)2+y2=2.
(Ⅱ)(x﹣1)2+y2=2.
【解析】试题分析:(Ⅰ)先设出椭圆的方程,根据题设中的焦距求得c和焦点坐标,根据点(1,![]() )到两焦点的距离求得a,进而根据b=
)到两焦点的距离求得a,进而根据b=![]() 求得b,得到椭圆的方程.
求得b,得到椭圆的方程.
(Ⅱ)先看当直线l⊥x轴,求得A,B点的坐标进而求得△AF2B的面积与题意不符故排除,进而可设直线l的方程为:y=k(x+1)与椭圆方程联立消y,设A(x1,y1),B(x2,y2),根据韦达定理可求得x1+x2和x1x2,进而根据表示出|AB|的距离和圆的半径,求得k,最后求得圆的半径,得到圆的方程.
解:(Ⅰ)设椭圆的方程为![]() ,由题意可得:
,由题意可得:
椭圆C两焦点坐标分别为F1(﹣1,0),F2(1,0).
∴![]() .
.
∴a=2,又c=1,b2=4﹣1=3,
故椭圆的方程为![]() .
.
(Ⅱ)当直线l⊥x轴,计算得到:
![]() ,
,![]() ,不符合题意.
,不符合题意.
当直线l与x轴不垂直时,设直线l的方程为:y=k(x+1),
由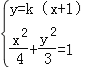 ,消去y得(3+4k2)x2+8k2x+4k2﹣12=0
,消去y得(3+4k2)x2+8k2x+4k2﹣12=0
显然△>0成立,设A(x1,y1),B(x2,y2),
则![]() ,
,
又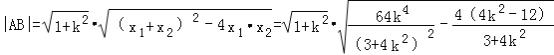
即![]() ,
,
又圆F2的半径![]() ,
,
所以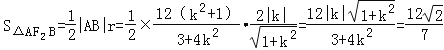 ,
,
化简,得17k4+k2﹣18=0,
即(k2﹣1)(17k2+18)=0,解得k=±1
所以,![]() ,
,
故圆F2的方程为:(x﹣1)2+y2=2.

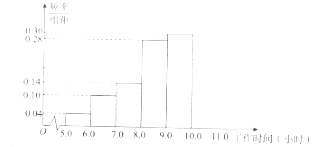
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 |
|
|
|
|
加工的时间 |
|
|
|
|
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(3)试预测加工![]() 个零件需要多少时间?
个零件需要多少时间?
附录:参考公式: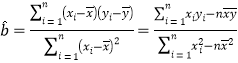 ,
,![]() .
.