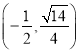题目内容
【题目】某校举行环保知识大奖赛，比赛分初赛和决赛两部分，初赛采用选手选一题答一题的方式进行，每位选手最多有5次选题答题的机会，选手累积答对3题或打错3题即终止其初赛的比赛：答对3题者直接进入初赛，打错3题者则被淘汰.已知选手甲答对每个问题的概率相同，并且相互之间没有影响，答题连续两次答错的概率为
.
（1）求选手甲可进入决赛的概率.
（2）设选手甲在初赛中答题的个数为
，试求
的分布列，并求
的数学期望.
【答案】（1）P
（2）见解析
【解析】试题分析： 
设选手甲任答一题，正确的概率为
，根据甲答对每个问题的概率相同，并且相互之间没有影响，答题连续两次打错的概率为
，列出关于
的方程，得到甲答对题目的概率，选手甲能够进入决赛包括两种情况，这两种情况是互斥的，由互斥事件的概率公式计算得到答案；
的取值为
， 
， 
，对应的事件分别是前三个题全部答对，前四个题答对了三个，其中第四题一定对，前五个题答对了三个，第五个一定答对，分别求出它们的概率，列出分布列，求出期望；
解析：（1）设选手甲任答一题，正确的概率为
，依题意
， 
，
选手甲可进入决赛的概率
.
（2）随机变量
所有可能取值为
， 
， 
，
依题意
，
，
，
故随机变量
的分布列为：
|
|
|
|
|
|
|
|
.
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
【题目】在高中学习过程中，同学们常这样说：“如果你的物理成绩好，那么你的数学学习就不会有什么大问题．”某班针对“高中物理学习对数学学习的影响”进行研究，得到了学生的物理成绩与数学成绩具有线性相关关系，如表为该班随机抽取6名学生在一次考试中的物理和数学成绩：
学生编号 学科 | 1 | 2 | 3 | 4 | 5 | 6 |
物理成绩（x） | 75 | 65 | 75 | 65 | 60 | 80 |
数学成绩（y） | 125 | 117 | 110 | 103 | 95 | 110 |
（1）求数学成绩y对物理成绩x的线性回归方程；
（2）该班某同学的物理成绩100分，预测他的数学成绩．
参考公式：回归方程
中斜率和截距的最小二乘估计公式分别为：
，
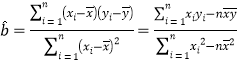参考数据：752+652+752+652+602+802＝29700，
75×125+65×117+75×110+65×103+60×95+80×110＝46425．
