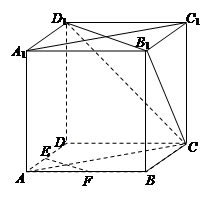
题目内容
在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.

(1)证明:连结BD.
在长方体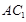 中,对角线BD∥B
中,对角线BD∥B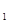 D
D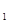
又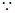 E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点,
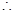 EF∥BD.
EF∥BD. 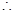 EF∥B
EF∥B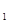 D
D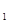
又B1D1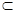 平面
平面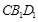 , EF
, EF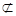 平面
平面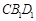 ,
,
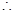 EF∥平面CB1D1. ………………………………7分
EF∥平面CB1D1. ………………………………7分
(2) 在长方体
在长方体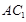 中,AA1⊥平面A1B1C1D1,而B1D1
中,AA1⊥平面A1B1C1D1,而B1D1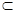 平面A1B1C1D1,
平面A1B1C1D1,
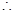 AA1⊥B1D1.
AA1⊥B1D1.
又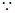 在正方形A1B1C1D1中,A1C1⊥B1D1,
在正方形A1B1C1D1中,A1C1⊥B1D1,
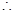 B1D1⊥平面CAA1C1.
B1D1⊥平面CAA1C1.
又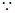 B1D1
B1D1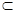 平面CB1D1,
平面CB1D1,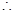 平面CAA1C1⊥平面CB1D1.
平面CAA1C1⊥平面CB1D1.
在长方体
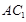 中,对角线BD∥B
中,对角线BD∥B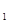 D
D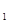
又
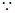 E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点,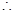 EF∥BD.
EF∥BD. 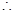 EF∥B
EF∥B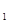 D
D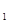
又B1D1
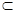 平面
平面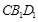 , EF
, EF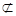 平面
平面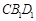 ,
,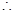 EF∥平面CB1D1. ………………………………7分
EF∥平面CB1D1. ………………………………7分(2)
 在长方体
在长方体 中,AA1⊥平面A1B1C1D1,而B1D1
中,AA1⊥平面A1B1C1D1,而B1D1 平面A1B1C1D1,
平面A1B1C1D1, AA1⊥B1D1.
AA1⊥B1D1.又
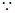 在正方形A1B1C1D1中,A1C1⊥B1D1,
在正方形A1B1C1D1中,A1C1⊥B1D1,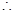 B1D1⊥平面CAA1C1.
B1D1⊥平面CAA1C1. 又
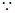 B1D1
B1D1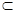 平面CB1D1,
平面CB1D1, 平面CAA1C1⊥平面CB1D1.
平面CAA1C1⊥平面CB1D1.略

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
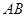 与
与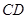 的位置关系为( )
的位置关系为( )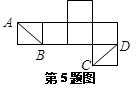
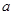 //直线
//直线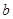 ,直线
,直线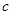 与
与 分别相交于点
分别相交于点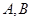 , 求证:
, 求证: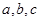 三条直线共面.
三条直线共面.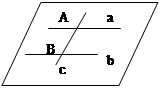
 中,侧棱
中,侧棱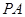 与底面
与底面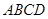 所成角的正切值为
所成角的正切值为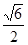 .
.  与底面
与底面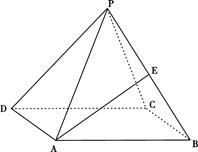
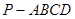 的底面
的底面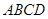 是边长为
是边长为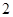 的正方形,
的正方形,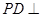 底面
底面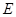 、
、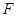 分别为棱
分别为棱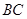 、
、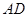 的中点.
的中点.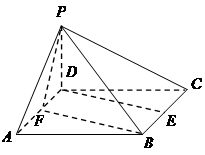
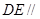 平面
平面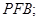
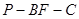 的余弦值为
的余弦值为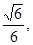 求四棱锥
求四棱锥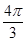 ,则此球的表面积为 .
,则此球的表面积为 .
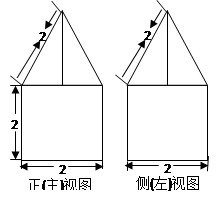
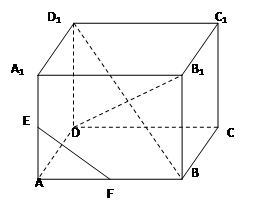

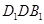 ;
;