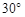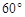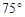题目内容
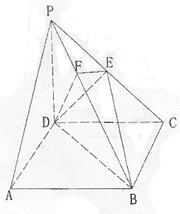
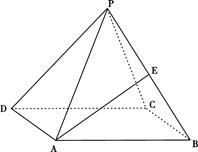
如图,正四棱锥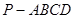 中,侧棱
中,侧棱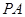 与底面
与底面 所成角的正切值为
所成角的正切值为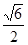 .
.
(1)求侧面 与底面
与底面 所成二面角的大小;
所成二面角的大小;
(2)若E是PB中点,求异面直线PD与AE所成角的正切值.
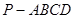 中,侧棱
中,侧棱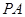 与底面
与底面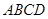 所成角的正切值为
所成角的正切值为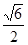 .
. (1)求侧面
 与底面
与底面 所成二面角的大小;
所成二面角的大小;(2)若E是PB中点,求异面直线PD与AE所成角的正切值.

(1)连结AC,BD交于点O,连结PO,则PO⊥面ABCD,
∴ ∠PAO就是PA与底面ABCD所成的角,∴ tan∠PAO=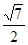 .
.
设AB=1,则PO=AOtan∠PAO =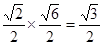 .
.
设F为AD中点,连FO、PF,
易知OF⊥AD,PF⊥AD,所以∠PAO就是侧面PAD与底面ABCD所成二面角的平面角.
在Rt 中,
中,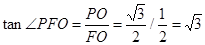 ,
,
∴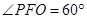 ,即侧面PAD与底面ABCD所成二面角的大小为
,即侧面PAD与底面ABCD所成二面角的大小为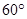 ;
;
(2)连结EO,由于O为BD中点,E为PD中点,所以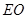
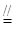
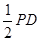 .
.
∴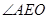 就是异面直线PD与AE所成的角.
就是异面直线PD与AE所成的角.
在Rt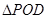 中,
中,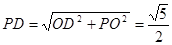 .∴
.∴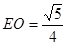 .
.
由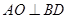 ,
,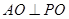 可知
可知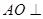 面
面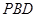 .所以
.所以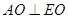 ,
,
在Rt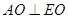 中,
中,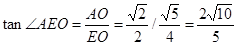 ,
,
即异面直线PD与AE所成角的正切值为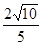 .
.
∴ ∠PAO就是PA与底面ABCD所成的角,∴ tan∠PAO=
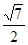 .
. 设AB=1,则PO=AOtan∠PAO =
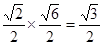 .
. 设F为AD中点,连FO、PF,
易知OF⊥AD,PF⊥AD,所以∠PAO就是侧面PAD与底面ABCD所成二面角的平面角.
在Rt
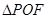 中,
中,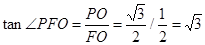 ,
,∴
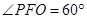 ,即侧面PAD与底面ABCD所成二面角的大小为
,即侧面PAD与底面ABCD所成二面角的大小为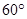 ;
;(2)连结EO,由于O为BD中点,E为PD中点,所以
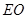
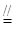
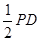 .
.∴
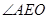 就是异面直线PD与AE所成的角.
就是异面直线PD与AE所成的角. 在Rt
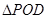 中,
中,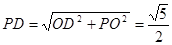 .∴
.∴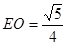 .
. 由
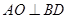 ,
,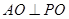 可知
可知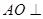 面
面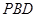 .所以
.所以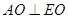 ,
, 在Rt
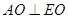 中,
中,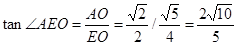 ,
,即异面直线PD与AE所成角的正切值为
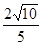 .
.略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
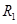 ,能容纳得下此框架的最小球的半径为
,能容纳得下此框架的最小球的半径为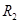 . 则
. 则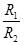 等于_______________.
等于_______________.
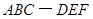 中,
中, 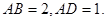
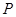 是
是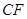 的沿长线上一点,
的沿长线上一点,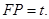 过
过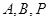 三点的平面交
三点的平面交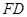 于
于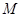 ,交
,交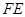 于
于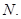
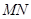 ∥平面
∥平面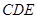 ;
;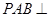 平面
平面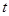 的值.
的值.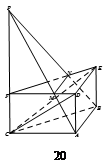
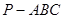 中,底面
中,底面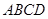 是正方形,侧棱
是正方形,侧棱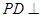 底面
底面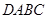 ,
,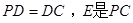 的中点,作
的中点,作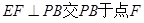
 ;
;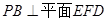 ;
;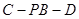 的大小。
的大小。