题目内容
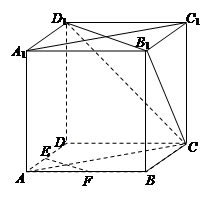
如图已知正四棱柱ABCD----A1B1C1D1,AB=1,AA1=2,点E为CC1的中点,点F为BD1的中点。

(1)证明:EF⊥平面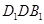 ;
;
(2)求点A1到平面BDE的距离;
(3)求BD1与平面BDE所成的角的余弦值.

(1)证明:EF⊥平面
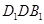 ;
;(2)求点A1到平面BDE的距离;
(3)求BD1与平面BDE所成的角的余弦值.
(1) 以D为原点,DA、DC、AA1所在直线为X、Y、Z轴建立空间直角坐标系.
D(0,0,0),B(1,1,0)
D1(0,0,2),E(0,1,1),F(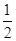 ,
,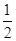 ,1)
,1)
∴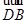 =(1,1,0),
=(1,1,0),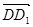 =(0,0,2),
=(0,0,2),
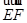 =(
=(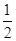 ,-
,-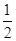 ,0) 由
,0) 由 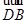 ·
·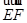 =0,
=0,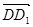 ·
·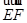 =0,
=0,
得,EF⊥DB,EF⊥DD1 ∴EF⊥面D1DB1----------------------------------------------------
(2) 设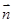 =(x,y,z)是平面BDE的法向量,
=(x,y,z)是平面BDE的法向量,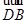 =(1,1,0),
=(1,1,0),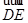 =(0,1,1)
=(0,1,1)
由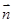 ⊥
⊥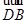 ,
, 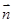 ⊥
⊥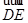 得
得 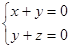 即
即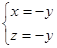
∴取y=1,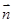 =(-1,1,-1)
=(-1,1,-1)
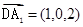 ,由(2)知点
,由(2)知点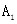 到平面BDE的距离为
到平面BDE的距离为 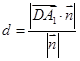 =
=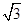 ----
----
(3)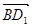 =(-1,-1,2)
=(-1,-1,2)
由(2)知
设直线BD1与平面BDE所成的角的正弦值为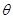 ,则sin
,则sin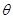 =
=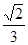 ,cos
,cos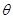 =
=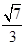
∴直线BD1与平面BDE所成的角的余弦值为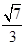 --------------------
--------------------
D(0,0,0),B(1,1,0)
D1(0,0,2),E(0,1,1),F(
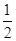 ,
,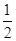 ,1)
,1) ∴
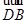 =(1,1,0),
=(1,1,0),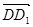 =(0,0,2),
=(0,0,2),
|
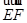 =(
=(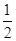 ,-
,-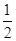 ,0) 由
,0) 由 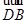 ·
·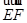 =0,
=0,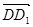 ·
·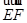 =0,
=0,得,EF⊥DB,EF⊥DD1 ∴EF⊥面D1DB1----------------------------------------------------
(2) 设
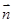 =(x,y,z)是平面BDE的法向量,
=(x,y,z)是平面BDE的法向量,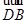 =(1,1,0),
=(1,1,0),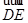 =(0,1,1)
=(0,1,1)由
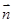 ⊥
⊥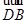 ,
, 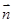 ⊥
⊥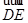 得
得 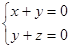 即
即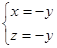
∴取y=1,
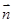 =(-1,1,-1)
=(-1,1,-1)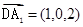 ,由(2)知点
,由(2)知点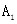 到平面BDE的距离为
到平面BDE的距离为 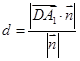 =
=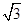 ----
----(3)
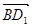 =(-1,-1,2)
=(-1,-1,2)由(2)知

设直线BD1与平面BDE所成的角的正弦值为
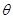 ,则sin
,则sin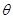 =
=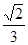 ,cos
,cos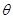 =
=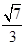
∴直线BD1与平面BDE所成的角的余弦值为
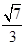 --------------------
--------------------略

练习册系列答案
相关题目
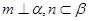 .下面有四个命题( )
.下面有四个命题( )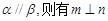 ; (2)
; (2)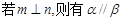 ;
;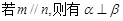 ; (4)
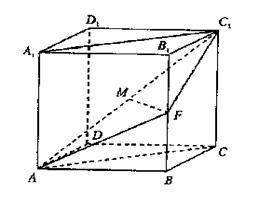
; (4)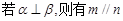 .
.
 为圆
为圆 的直径,点
的直径,点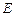 、
、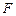 在圆
在圆 ,矩形
,矩形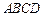 所在的平面和圆
所在的平面和圆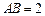 ,
,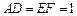 .
.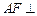 平面
平面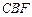 ;
;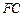 的中点为
的中点为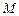 ,求证:
,求证: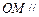 平面
平面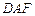 ;
;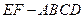 分割成的两个锥体的体积分别为
分割成的两个锥体的体积分别为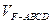 、
、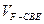 ,求
,求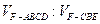 的值
的值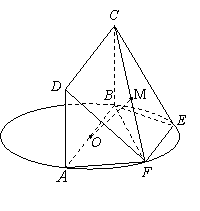
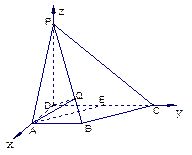
 中,侧棱
中,侧棱 ,底面
,底面 是直角梯形,
是直角梯形,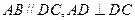 ,且
,且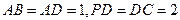 ,
,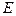 是
是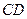 的中点.
的中点.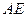 与
与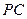 所成的角;
所成的角;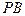 上是否存在一点
上是否存在一点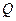 ,使得
,使得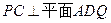 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
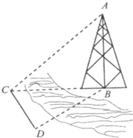
的值;若不存在,请说明理由.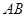 时,可以选与塔底
时,可以选与塔底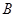 在同一水平面内的两个测点
在同一水平面内的两个测点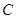 与
与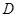 ,测得
,测得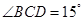 .
.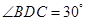 ,
,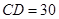 米,并在点
米,并在点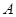 的仰角为
的仰角为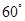 ,则塔高
,则塔高