Question

【题目】如图,在四棱锥中,平面,底面为菱形,且,E为的中点.

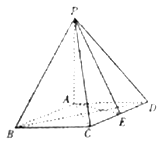
(1)求证:平面平面;

(2)棱上是否存在点F,使得平面?说明理由.

Answer 1

【答案】(1)见解析(2)存在点F为中点,见解析

【解析】

(1)由 及菱形的性质可得，再由平面,平面,所以，可得平面，可得证明；

(2) 分别取,的中点F,G,连接,易得且，且，四边形为平行四边形,所以可得平面.

解:(1)证明:因为底面是菱形且,所以为正三角形,

因为E为的中点,所以,

因为,所以;

因为平面,平面,

所以;

因为.

所以平面,

平面,所以平面平面.

(2)存在点F为中点时,满足平面;理由如下:

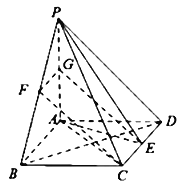
分别取,的中点F,G,连接,

在三角形中,且;

在菱形中,E为中点,所以且,

所以且,即四边形为平行四边形,

所以;

又平面,平面,所以平面.