题目内容
(本小题满分12分)
在平面直角坐标系xOy中,曲线y=x2-2x—3与两条坐标轴的三个交点都在圆C上.若圆C与直线x-y+a=0交于A,B两点,
(1)求圆C的方程;
(2)若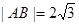 ,求a的值;
,求a的值;
(3)若 OA⊥OB,(O为原点),求a的值.
在平面直角坐标系xOy中,曲线y=x2-2x—3与两条坐标轴的三个交点都在圆C上.若圆C与直线x-y+a=0交于A,B两点,
(1)求圆C的方程;
(2)若
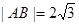 ,求a的值;
,求a的值;(3)若 OA⊥OB,(O为原点),求a的值.
(1) (x-1)2+(y+1)2=5. (2)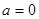 或
或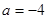 ;(3) a=-1.
;(3) a=-1. 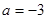 。
。
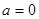 或
或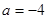 ;(3) a=-1.
;(3) a=-1. 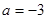 。
。试题分析:(1)曲线y=x2-2x—3与y轴的交点为(0,-3),与x轴的交点为(-1,0),(3,0).
故可设圆C的圆心为(1,t),则有12+(t+3)2=(1+1)2+t2,解得t=
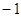 .
. 则圆C的半径为
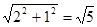 .则以圆C的方程为(x-1)2+(y+1)2=5.
.则以圆C的方程为(x-1)2+(y+1)2=5. (2)
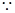
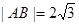 ,
, 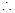 圆心C到直线x-y+a=0的距离为
圆心C到直线x-y+a=0的距离为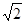
即
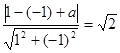 ,解得
,解得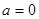 或
或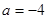
(3)设A(x1,y1),B(x2,y2),其坐标满足方程组:
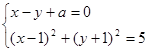 .
.消去y,得到方程2x2+2ax+a2+2a-3=0. 由已知可得,判别式Δ=24-16a-4a2>0.
从而x1+x2=-a,x1x2=
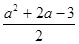 .①
.①由于OA⊥OB,可得x1x2+y1y2=0,又y1=x1+a,y2=x2+a,
所以2x1x2+a(x1+x2)+a2=0.②
由①,②得a=1,
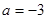 ,满足Δ>0,故a=-1.
,满足Δ>0,故a=-1. 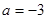
点评:典型题,关于圆的考查,往往以这种“连环题”的形式出现,首先求标准方程,往往不难。而涉及在直线与圆的位置关系,往往要利用韦达定理,实现“整体代换”。本题中利用OA⊥OB,可得x1x2+y1y2=0,从而将两根之积代入,方便求解。

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
 ,在上任取一点
,在上任取一点 ,线段
,线段 长度的最小值称为点
长度的最小值称为点 .设是长为2的线段,点集
.设是长为2的线段,点集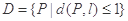 所表示图形的面积为( )
所表示图形的面积为( )

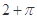

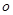 上一点
上一点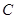 在直径
在直径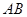 上的射影为
上的射影为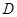 ,且
,且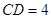 ,
,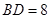 ,则⊙
,则⊙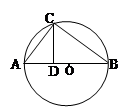
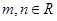 ,若直线
,若直线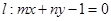 与
与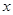 轴相交于点
轴相交于点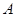 ,与
,与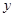 轴相交于
轴相交于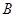 ,且
,且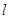 与圆
与圆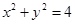 相交所得弦的长为2,
相交所得弦的长为2,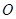 为坐标原点,求
为坐标原点,求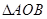 面积的最小值.
面积的最小值. 中,设二次函数
中,设二次函数 的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求: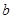 的取值范围;
的取值范围;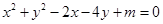 .
.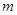 的取值范围;
的取值范围;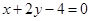 相交于
相交于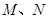 两点,且
两点,且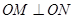 (
(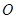 为坐标原点)求
为坐标原点)求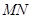 为直径的圆的方程.
为直径的圆的方程.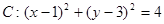 ,过原点
,过原点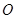 的直线
的直线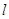 与圆
与圆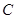 相交于
相交于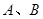 两点
两点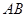 的长为
的长为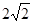 ,求直线
,求直线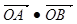 为定值。
为定值。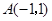 出发经
出发经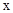 轴反射,到达圆C:
轴反射,到达圆C: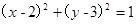 上一点的最短路程是( )
上一点的最短路程是( ) -1
-1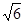
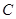 以
以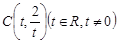 为圆心且经过原点O.
为圆心且经过原点O.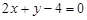 与圆
与圆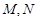 ,若
,若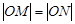 ,求圆
,求圆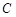 的方程;
的方程;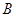 的坐标为
的坐标为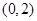 ,设
,设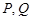 分别是直线
分别是直线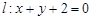 和圆
和圆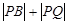 的最小值及此时点
的最小值及此时点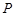 的坐标。
的坐标。