题目内容
【题目】某校参加高一年级期中考试的学生中随机抽出60名学生,将其数学成绩分成六段![]() 、
、![]() 、
、![]() 、
、![]() 后得到如图部分频率分布直方图,观察图形的信息,回答下列问题:
后得到如图部分频率分布直方图,观察图形的信息,回答下列问题:

![]() 求分数在
求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
![]() 统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
![]() 若从60名学生中随抽取2人,抽到的学生成绩在
若从60名学生中随抽取2人,抽到的学生成绩在![]() 记0分,在
记0分,在![]() 记1分,在
记1分,在![]() 记2分,用
记2分,用![]() 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)见解析;(2) 平均分为71(3)见解析
【解析】
![]() 根据概率之和为1,即频率分布直方图的面积之和为1.
根据概率之和为1,即频率分布直方图的面积之和为1.
![]() 根据题意同一组数据常用该组区间的中点值作为代表,所以用每一组数据的中点值代表这一组数的平均数,即可求得.
根据题意同一组数据常用该组区间的中点值作为代表,所以用每一组数据的中点值代表这一组数的平均数,即可求得.
![]() 从60名学生中随抽取2人,根据题意总记分可能为0、1、2、3、
从60名学生中随抽取2人,根据题意总记分可能为0、1、2、3、![]() 求出相应的概率,即可求得分布列和期望.
求出相应的概率,即可求得分布列和期望.
![]() 设分数在
设分数在![]() 内的频率为x,根据频率分布直方图,
内的频率为x,根据频率分布直方图,

有![]() ,
,
可得![]() ,所以频率分布直方图如图所示
,所以频率分布直方图如图所示
![]() 平均分为
平均分为
![]() 学生成绩在
学生成绩在![]() 的有
的有![]() 人,
人,
在![]() 的有
的有![]() 人,
人,
在![]() 的有
的有![]() 人,
人,
![]() 的可能取值是0,1,2,3,4
的可能取值是0,1,2,3,4
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 | 4 |
P |
|
|
| |
|
![]() .
.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案【题目】某媒体为调查喜爱娱乐节目![]() 是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
喜欢节目A | 不喜欢节目A | 总计 | |
男性观众 | |||
女性观众 | |||
总计 |
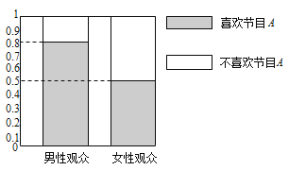
(1)根据该等高条形图,完成右上![]() 列联表,并用独立性检验的方法分析,则在犯错误的概率不超过多少的前提下认为喜欢娱乐节目
列联表,并用独立性检验的方法分析,则在犯错误的概率不超过多少的前提下认为喜欢娱乐节目![]() 与观众性别有关?
与观众性别有关?
(2)从男性观众中按喜欢节目![]() 与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目
与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目![]() 和1名不喜欢节目
和1名不喜欢节目![]() 的概率.
的概率.
附: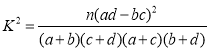
| 0.100 | 0.050 | 0.010 | 0.00 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】随着移动支付的普及,中国人的生活方式正悄然巨变,带智能手机,不带钱包出门还渐成为中国人的新习惯![]() 年我国移动支付增长迅猛,据统计,某支付平台2017年移动支付的笔数占总支付笔数的
年我国移动支付增长迅猛,据统计,某支付平台2017年移动支付的笔数占总支付笔数的![]() .
.
![]() Ⅰ
Ⅰ![]() 从该支付平台2017年的所有支付中任取10笔,求移动支付笔数的期望和方差;
从该支付平台2017年的所有支付中任取10笔,求移动支付笔数的期望和方差;
![]() Ⅱ
Ⅱ![]() 现有500名使用该支付平台的用户,其中300名是城市用户,200名是农村用户,调查他们2017年个人移动支付的比例是否达到了
现有500名使用该支付平台的用户,其中300名是城市用户,200名是农村用户,调查他们2017年个人移动支付的比例是否达到了![]() ,得到
,得到![]() 列联表如下:
列联表如下:
个人移动支付达到了 | 个人移动支付达到了 | 合计 | |
城市用户 | 270 | 30 | 300 |
农村用户 | 170 | 30 | 200 |
合计 | 440 | 60 | 500 |
根据上表数据,问是否有![]() 的把握认为2017年个人移动支付比例达到了
的把握认为2017年个人移动支付比例达到了![]() 与该用户是城市用户还是农村用户有关?
与该用户是城市用户还是农村用户有关?
附:![]()
|
|
|
k |
|
|
【题目】在一次恶劣气候的飞行航程中调查男女乘客在飞机上晕机的情况,共调查了89位乘客,其中男乘客有24人晕机,31人不晕机;女乘客有8人晕机,26人不晕机
(1)根据此材料数据完成如下的2×2列联表;
晕机 | 不晕机 | 总计 | |
男人 | |||
女人 | |||
总计 |
(2)根据列联表,利用下列公式和数据分析,你是否有90%的把握认为在本次飞机飞行中晕机与性别有关?
(3)其中8名晕机的女乘客中有5名是常坐飞机的乘客,另外3名是不常坐飞机的,从这8名乘客中任选3名,这3名乘客不都是常坐飞机的概率是多少?
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式: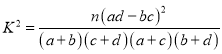 ,其中
,其中![]()