题目内容
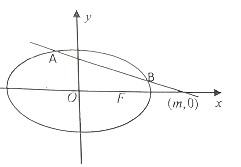
【题目】已知椭圆![]() 的右焦点F与抛物线
的右焦点F与抛物线![]() 焦点重合,且椭圆的离心率为
焦点重合,且椭圆的离心率为![]() ,过
,过![]() 轴正半轴一点
轴正半轴一点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点.
两点.
(1)求椭圆的标准方程;
(2)是否存在实数![]() 使以线段
使以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,若存在,求出实数
,若存在,求出实数![]() 的值;若不存在说明理由.
的值;若不存在说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() .
.
【解析】
(1)根据抛物线焦点可得![]() ,又根据离心率可求
,又根据离心率可求![]() ,利用
,利用![]() ,即可写出椭圆的方程
,即可写出椭圆的方程
(2)由题意可设直线![]() 的方程为
的方程为![]() ,联立方程组,消元得一元二次方程,写出
,联立方程组,消元得一元二次方程,写出![]() ,利用根与系数的关系可求存在m.
,利用根与系数的关系可求存在m.
解:(1)![]() 抛物线
抛物线![]() 的焦点是
的焦点是![]()
![]() ,
,![]() ,又
,又![]() 椭圆的离心率为
椭圆的离心率为![]() ,即
,即![]()
![]() ,
,![]() ,则
,则![]()
故椭圆的方程为![]() .
.
(2)由题意得直线![]() 的方程为
的方程为![]()
由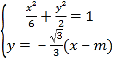 消去
消去![]() 得
得![]() .
.
由![]() ,解得
,解得![]() .
.
又![]() ,
,![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
![]() .
.
![]() ,
,![]() ,
,
![]()
若存在![]() 使以线段
使以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,则必有
,则必有![]() ,即
,即![]() ,
,
解得![]() .又
.又![]() ,
,![]() .
.
即存在![]() 使以线段
使以线段![]() 为直径的圆经过点.
为直径的圆经过点.

练习册系列答案
相关题目
【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见下表.
内,发布成绩使用等级制,各等级划分标准见下表.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定:A,B,C三级为合格等级,D为不合格等级为了解该校高三年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
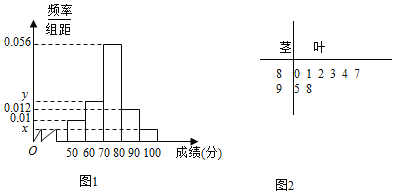
![]() 求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
![]() 根据频率分布直方图,求成绩的中位数
根据频率分布直方图,求成绩的中位数![]() 精确到
精确到![]() ;
;
![]() 在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.