题目内容
【题目】如图,四棱锥![]() 中,
中,![]() 底面ABCD,
底面ABCD,![]() ,
,![]() ,
,![]() .
.
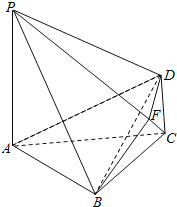
![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面PAC;
平面PAC;
![]() Ⅱ
Ⅱ![]() 若侧棱PC上的点F满足
若侧棱PC上的点F满足![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析 (2)![]()
【解析】
试题(1)由于![]() 可以证明
可以证明![]() 要证明
要证明![]() 只需证明
只需证明![]() 从而
从而![]() 中的两条相交直线,
中的两条相交直线,![]() (2)由(1)知
(2)由(1)知![]() 为等腰三角形,面积容易求出,考虑以BCD为底面.F为顶点 的三棱锥,以及以BCD为底面,P为顶点的三棱锥面积容易求出,所以
为等腰三角形,面积容易求出,考虑以BCD为底面.F为顶点 的三棱锥,以及以BCD为底面,P为顶点的三棱锥面积容易求出,所以![]()
试题解析:(1)证明:因为BC=CD,所以△BCD为等腰三角形,
又∠ACB=∠ACD,故BD⊥AC. 因为PA⊥底面ABCD,所以PA⊥BD.
从而BD与平面PAC内两条相交直线PA,AC都垂直, 所以BD⊥平面PAC.
(2)解:三棱锥PBCD的底面BCD的面积S△BCD=![]() BC·CD·sin∠BCD=
BC·CD·sin∠BCD=![]() ×2×2×sin
×2×2×sin![]() =
=![]() .
.
由PA⊥底面ABCD,得![]() =
=![]() ·S△BCD·PA=
·S△BCD·PA=![]() ×
×![]() ×2
×2![]() =2.
=2.
由PF=7FC,得三棱锥FBCD的高为![]() PA,
PA,
故![]() =
=![]() ·S△BCD·
·S△BCD·![]() PA=
PA=![]() ×
×![]() ×
×![]() ×2
×2![]() =
=![]() ,
,
所以![]() =
=![]() -
-![]() =2-
=2-![]() =
=![]() .
.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目


