题目内容
【题目】已知函数![]() 在点
在点![]() 处取得极值
处取得极值![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 有极大值
有极大值![]() ,求
,求![]() 在
在![]() 上的最小值.
上的最小值.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1) 函数![]() 在点
在点![]() 处取得极值
处取得极值![]() ,则
,则![]() ,
, ![]() ,列方程组解出a,b的值即可;(2)对函数求导判断单调性,求出函数的极大值,由极大值
,列方程组解出a,b的值即可;(2)对函数求导判断单调性,求出函数的极大值,由极大值![]() 可求出c的值,代回解析式,根据单调性求出函数
可求出c的值,代回解析式,根据单调性求出函数![]() 在
在![]() 上的最小值.
上的最小值.
试题解析:
(1)因f(x)=ax3+bx+c,故f′(x)=3ax2+b,
由于f(x)在点x=2处取得极值c-16,
故有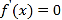 ,
,
即![]() 化简得
化简得![]() ,
,
解得a=1,b=-12.
(2)由(1)知f(x)=x3-12x+c;
f′(x)=3x2-12=3(x-2)(x+2).
令f′(x)=0,得x1=-2,x2=2.
当x∈(-∞,-2)时,f′(x)>0,故f(x)在(-∞,-2)上为增函数;
当x∈(-2,2)时,f′(x)<0,故f(x)在(-2,2)上为减函数;
当x∈(2,+∞)时,f′(x)>0,
故f(x)在(2,+∞)上为增函数.
由此可知f(x)在x1=-2处取得极大值f(-2)=16+c,f(x)在x1=2处取得极小值f(2)=c-16.
由题设条件知16+c=28得c=12.
此时f(-3)=9+c=21,f(3)=-9+c=3,
f(2)=-16+c=-4,
因此f(x)在[-3,3]上的最小值为f(2)=-4.
点睛: 函数的导数与极值点的关系:(1)定义域![]() 上的可导函数
上的可导函数![]() 在
在![]() 处取得极值的充要条件是
处取得极值的充要条件是![]() ,并且
,并且![]() 在
在![]() 两侧异号,若左负右正为极小值点,若左正右负为极大值点;(2)函数
两侧异号,若左负右正为极小值点,若左正右负为极大值点;(2)函数![]() 在点
在点![]() 处取得极值时,它在这点的导数不一定存在,例如函数
处取得极值时,它在这点的导数不一定存在,例如函数![]() ,结合图象,知它在
,结合图象,知它在![]() 处有极小值,但它在
处有极小值,但它在![]() 处的导数不存在;(3)
处的导数不存在;(3) ![]() 既不是函数
既不是函数![]() 在
在![]() 处取得极值的充分条件也不是必要条件.最后一定要注意对极值点进行检验.
处取得极值的充分条件也不是必要条件.最后一定要注意对极值点进行检验.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案【题目】已知函数![]() 的定义域为[-1,5],部分对应值如下表,
的定义域为[-1,5],部分对应值如下表, ![]() 的导函数
的导函数![]() 的图象如图所示,下列关于
的图象如图所示,下列关于![]() 的命题:
的命题:

| -1 | 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
①函数![]() 的极大值点为0,4;
的极大值点为0,4;
②函数![]() 在[0,2]上是减函数;
在[0,2]上是减函数;
③如果当![]() 时,
时, ![]() 的最大值是2,那么t的最大值为4;
的最大值是2,那么t的最大值为4;
④当1<a<2时,函数![]() 有4个零点.
有4个零点.
其中正确命题的序号是__________.
【题目】10月1日,某品牌的两款最新手机(记为![]() 型号,
型号,![]() 型号)同时投放市场,手机厂商为了解这两款手机的销售情况,在10月1日当天,随机调查了5个手机店中这两款手机的销量(单位:部),得到下表:
型号)同时投放市场,手机厂商为了解这两款手机的销售情况,在10月1日当天,随机调查了5个手机店中这两款手机的销量(单位:部),得到下表:
手机店 |
|
|
|
|
|
| 6 | 6 | 13 | 8 | 11 |
| 12 | 9 | 13 | 6 | 4 |
(Ⅰ)若在10月1日当天,从![]() ,
,![]() 这两个手机店售出的新款手机中各随机抽取1部,求抽取的2部手机中至少有一部为
这两个手机店售出的新款手机中各随机抽取1部,求抽取的2部手机中至少有一部为![]() 型号手机的概率;
型号手机的概率;
(Ⅱ)现从这5个手机店中任选3个举行促销活动,用![]() 型号手机销量超过
型号手机销量超过![]() 型号手机销量的手机店的个数,求随机变量
型号手机销量的手机店的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(III)经测算,![]() 型号手机的销售成本
型号手机的销售成本![]() (百元)与销量(部)满足关系
(百元)与销量(部)满足关系![]() .若表中
.若表中![]() 型号手机销量的方差
型号手机销量的方差![]() ,试给出表中5个手机店的
,试给出表中5个手机店的![]() 型号手机销售成本的方差
型号手机销售成本的方差![]() 的值.(用
的值.(用![]() 表示,结论不要求证明)
表示,结论不要求证明)