Question

18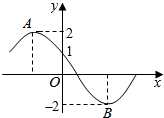．如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，0≤φ≤π）的部分图象，其中A，B两点之间的距离为5．
（1）求函数f（x）的解析式；
（2）判断函数f（x）在区间[$\frac{7}{4}$，$\frac{9}{4}$]上是否存在对称轴，存在求出方程；否则说明理由．

Answer 1

分析 （1）由图象得到振幅A，由A、B两点的距离结合勾股定理求出B和A的横坐标的差，即半周期，然后求出ω，再由f（0）=1求φ的值，则解析式可求．
（2）由$\frac{π}{3}$x+$\frac{5π}{6}$=kπ+$\frac{π}{2}$，k∈Z．可解得对称轴方程．

解答 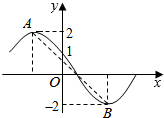解：（1）由图象可知，A=2．
又A，B两点之间的距离为5，A，B两点的纵坐标的差为4，得函数的半个周期$\frac{T}{2}=3$，∴T=6．
则ω=$\frac{2π}{T}$=$\frac{2π}{6}$=$\frac{π}{3}$．
∴函数解析式为f（x）=2sin（$\frac{π}{3}$x+φ）．
由f（0）=1，得2sinφ=1，
∴sinφ=$\frac{1}{2}$．
又0≤φ≤π，
∴φ=$\frac{π}{6}$（舍去，（0，1）在单调递减的区间上，）或$\frac{5π}{6}$．
则f（x）=2sin（$\frac{π}{3}$x+$\frac{5π}{6}$）．
（2）由$\frac{π}{3}$x+$\frac{5π}{6}$=kπ+$\frac{π}{2}$，k∈Z，可解得：x=3k-1，k∈Z，
由3k-1∈[$\frac{7}{4}$，$\frac{9}{4}$]，解得：$\frac{11}{12}$≤k≤$\frac{13}{12}$，k∈Z，即解得k=1，
故函数f（x）=2sin（$\frac{π}{3}$x+$\frac{5π}{6}$）在区间[$\frac{7}{4}$，$\frac{9}{4}$]上存在对称轴，对称轴方程为：x=2；

点评 本题考查了由函数y=Asin（ωx+φ）的部分图象求函数解析式，正弦函数的图象和性质，解决此类问题的方法是先由图象看出振幅和周期，由周期求出ω，然后利用五点作图的某一点求φ，属于基本知识的考查．