题目内容
3.设x∈R.若[x]表示不超过x的最大整数,则f(x)=[x](1)求[3.5]+[4.2]
(2)试写出x∈[-2,2]时,f(x)的解析式;
(3)画出[-2,2]上函数f(x)的图象.
分析 (1)直接利用函数的定义求解即可.
(2)直接利用分段函数写出红丝带解析式即可.
(3)集合函数的解析式,直接画出函数的图象即可.
解答 解:若[x]表示不超过x的最大整数,则f(x)=[x]
(1)[3.5]+[4.2]=3+4=7.
(2)x∈[-2,-1)时,f(x)=-2;
x∈[-1,0)时,f(x)=-1;
x∈[0,1)时,f(x)=0;
x∈[1,2)时,f(x)=1;
x=2时,f(x)=2.
即f(x)=$\left\{\begin{array}{l}-2,x∈[-2,-1)\\-1,x∈[-1,0)\\ 0,x∈[0,1)\\ 1,x∈[1,2)\\ 2,x=2\end{array}\right.$
(3)x∈[-2,2],函数f(x)=$\left\{\begin{array}{l}-2,x∈[-2,-1)\\-1,x∈[-1,0)\\ 0,x∈[0,1)\\ 1,x∈[1,2)\\ 2,x=2\end{array}\right.$
的图象.如图: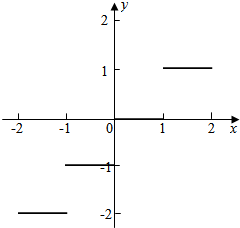
点评 本题考查函数解析式的确定,考查学生的作图能力,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.2015年春节放假安排,农历除夕至正月初六放假,共7天,某单位安排7位员工值班,每人值班1天,每天安排1人,若甲不在除夕值班,乙不在正月初一值班,而且丙和甲在相邻的两天值班,则不同的安排方案共有( )
| A. | 1440种 | B. | 1360种 | C. | 1282种 | D. | 1128种 |
12.设集合A{x||x-5|≤6,x∈N*},集合B={x|x2-x-12<0},则A∩B=( )
| A. | [-1,4) | B. | [-1,4) | C. | {0,1,2,3} | D. | {1,2,3} |
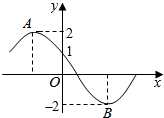 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5.
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5.