题目内容
9.已知a1=1,an+1=2an+1,cn=$\frac{{2}^{n}}{{a}_{n}•{a}_{n+1}}$,求证:c1+c2+…+cn<1.分析 由题意可得数列{an+1}是等比数列,由等比数列的通项公式求得an,代入cn=$\frac{{2}^{n}}{{a}_{n}•{a}_{n+1}}$后整理,然后利用裂项相消法求和证得答案.
解答 证明:由an+1=2an+1,得an+1+1=2(an+1),
∵a1=1,∴a1+1=1+1=2≠0,
则数列{an+1}是以2为首项,以2为公比的等比数列,
∴${a}_{n}+1={2}^{n}$,${a}_{n}={2}^{n}-1$.
∴cn=$\frac{{2}^{n}}{{a}_{n}•{a}_{n+1}}$=$\frac{{2}^{n}}{({2}^{n}-1)({2}^{n+1}-1)}$=$\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n+1}-1}$,
则c1+c2+…+cn =$(\frac{1}{{2}^{1}-1}-\frac{1}{{2}^{2}-1})+(\frac{1}{{2}^{2}-1}-\frac{1}{{2}^{3}-1})+…+$$(\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n+1}-1})$
=$\frac{1}{{2}^{1}-1}-\frac{1}{{2}^{n+1}-1}=1-\frac{1}{{2}^{n+1}-1}<1$.
点评 本题考查数列递推式,考查了等比关系的确定,训练了裂项相消法求数列的和,是中档题.

练习册系列答案
相关题目
19.函数y=lnx在点A(1,0)处的切线方程为( )
| A. | x-1-0 | B. | x+y-1=0 | C. | x-y-1=0 | D. | x-y+1=0 |
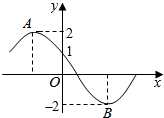 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5.
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5.