题目内容
8.已知数列{an}的前n项和为Sn,a1=1,2Sn+1-Sn=2,n∈N*.(1)求{an}的通项公式;
(2)设数列{an2}的前n项和为Tn,若Sn2-λTn<0对任意n∈N*恒成立,求实数λ的最小值.
分析 (1)由2Sn+1-Sn=2,n∈N*,变形为${S}_{n+1}-2=\frac{1}{2}({S}_{n}-2)$,利用等比数列的通项公式可得Sn-2,再利用递推式可得an.
(2)由(1)可得${a}_{n}^{2}$=$\frac{1}{{4}^{n-1}}$.kd 数列{an2}的前n项和为Tn=$\frac{4}{3}$$(1-\frac{1}{{4}^{n}})$.于是Sn2-λTn<0化为λ>3-$\frac{6}{{2}^{n}+1}$.再利用数列的单调性即可得出.
解答 解:(1)∵2Sn+1-Sn=2,n∈N*,
∴${S}_{n+1}-2=\frac{1}{2}({S}_{n}-2)$,
∴数列{Sn-2}是等比数列,首项为-1,公比为$\frac{1}{2}$.
∴Sn-2=-$\frac{1}{{2}^{n-1}}$,
∴Sn=2-$\frac{1}{{2}^{n-1}}$,
∴an=Sn-Sn-1=$(2-\frac{1}{{2}^{n-1}})$-$(2-\frac{1}{{2}^{n-2}})$=$\frac{1}{{2}^{n-1}}$.
(2)由(1)可得${a}_{n}^{2}$=$\frac{1}{{4}^{n-1}}$.
∴数列{an2}的前n项和为Tn=$\frac{1-\frac{1}{{4}^{n}}}{1-\frac{1}{4}}$=$\frac{4}{3}$$(1-\frac{1}{{4}^{n}})$.
Sn2-λTn<0即$(2-\frac{1}{{2}^{n-1}})^{2}$<λ•$\frac{4}{3}$$(1-\frac{1}{{4}^{n}})$.
化为λ>$\frac{3(1-\frac{1}{{2}^{n}})}{1+\frac{1}{{2}^{n}}}$=3-$\frac{6}{{2}^{n}+1}$.
∵数列$\{\frac{6}{{2}^{n}+1}\}$单调递减,且Sn2-λTn<0对任意n∈N*恒成立,
∴λ≥3.
∴λ的最小值为3.
点评 本题考查了递推式的应用、等比数列的通项公式、数列的单调性,考查了推理能力与计算能力,属于中档题.

| A. | 22013 | B. | 22014 | C. | 32013 | D. | 32014 |
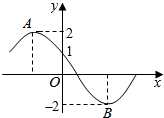 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5.
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5.