题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{kx+1,x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,下列是关于函数y=f[f(x)]+1的零点个数的4个判断:①当k>0时,有3个零点;
②当k<0时,有2个零点;
③当k>0时,有4个零点;
④当k<0时,有1个零点,
则正确的判断是③④.
分析 由y=0得f[f(x)]=-1,利用换元法将函数分解为f(x)=t和f(t)=-1,作出函数f(x)的图象,利用数形结合即可得到结论.
解答 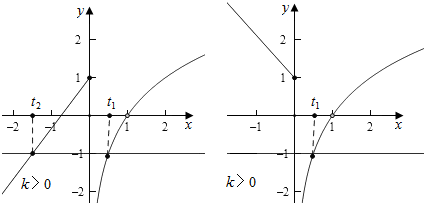 解答:解:由y=f[f(x)]+1=0得f[f(x)]+1=0,
解答:解:由y=f[f(x)]+1=0得f[f(x)]+1=0,
即f[f(x)]=-1,
设f(x)=t,
则方程f[f(x)]=-1
等价为f(t)=-1,
①若k>0,作出函数f(x)的图象如图
∵f(t)=-1,
∴此时方程f(t)=-1有两个根其中t2<0,0<t1<1,
由f(x)=t2<0,知此时x有两解,
由f(x)=t1∈(0,1)知此时x有两解,
此时共有4个解,即函数y=f[f(x)]+1有4个零点.
②若k<0,作出函数f(x)的图象如图:
∵f(t)=-1,
∴此时方程f(t)=-1有一个根t1,其中0<t1<1,
由f(x)=t1∈(0,1)知此时x只有1个解,
即函数y=f[f(x)]+1有1个零点.
综上:只有③④正确.
故答案为:③④.
点评 本题考查分段函数的应用,考查复合函数的零点的判断,利用换元法和数形结合是解决本题的关键.

练习册系列答案
相关题目
19.函数y=lnx在点A(1,0)处的切线方程为( )
| A. | x-1-0 | B. | x+y-1=0 | C. | x-y-1=0 | D. | x-y+1=0 |
20.已知函数f(x)=$\left\{\begin{array}{l}{|2x-1|,}&{x>0}\\{\frac{3}{2}x+2,}&{x≤0}\end{array}\right.$,若关于x的方程f(sinx)=m在区间[0,2π]上有四个不同的实数根,则实数m的取值范围是( )
| A. | 0<m<$\frac{1}{2}$ | B. | 0<m≤$\frac{1}{2}$ | C. | $\frac{1}{2}$<m≤1 | D. | $\frac{1}{2}$<m<1 |
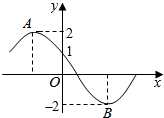 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5.
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5.