题目内容
13.已知等比数列{an}的前n项和为Sn=t•3n-2-$\frac{1}{3}$,则实数t的值为3.分析 当n≥2时,an=Sn-Sn-1,代入化简可得表达式,再由a1=S1和数列为等比数列可得t的方程,解方程可得.
解答 解:当n≥2时,an=Sn-Sn-1=(t•3n-2-$\frac{1}{3}$)-(t•3n-3-$\frac{1}{3}$)=2t•3n-3,
当n=1时,a1=S1=t•31-2-$\frac{1}{3}$=$\frac{1}{3}$(t-1),
∴2t•31-3=$\frac{1}{3}$(t-1),解得t=3,
故答案为:3.
点评 本题考查等比数列的求和公式,涉及分类讨论的思想,属基础题.

练习册系列答案
相关题目
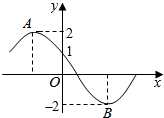 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5.
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5.