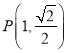Question

【题目】已知动点到点与点的距离之比为2，记动点的轨迹为曲线C.

(1)求曲线C的方程；

(2)过点作曲线C的切线，求切线方程．

Answer 1

【答案】(1)；(2) 或．

【解析】

(1)根据题意设出M点的坐标，然后根据距离之比等于2，化简出x，y的关系式，求出M的轨迹方程.(2)由第一问的结论可判断点在圆外，可知切线方程有两条，设出切线方程，根据圆心到直线的距离公式可求出斜率k的值，从而求出切线方程.

（1）设动点的坐标为，

则，

所以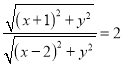，化简得，

因此，动点的轨迹方程为；

（2）∵圆心(3,0)到点(6,2)的距离为大于半径3，

∴点(-2,4)在已知圆外,过该点的圆的切线有两条

不妨设过该点的切线斜率为，

则切线方程为，即，

由圆心到直线的距离等于半径可知，，解得或．

所以，切线方程为或．