题目内容
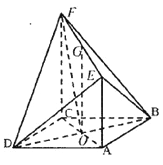
【题目】如图，在三棱锥P-ABC中，PA⊥底面ABC， 
.点D，E，N分别为棱PA，PC，BC的中点，M是线段AD的中点，PA=AC=4，AB=2.
（Ⅰ）求证：MN∥平面BDE；
（Ⅱ）求二面角C-EM-N的正弦值；
（Ⅲ）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为
，求线段AH的长.
【答案】（Ⅰ）见解析;（Ⅱ）
;（Ⅲ）
或
.
【解析】试题分析：本小题主要考查直线与平面平行、二面角、异面直线所成的角等基础知识.考查用空间向量解决立体几何问题的方法.考查空间想象能力、运算求解能力和推理论证能力.首先要建立空间直角坐标系，写出相关点的坐标，证明线面平行只需求出平面的法向量，计算直线对应的向量与法向量的数量积为0，求二面角只需求出两个半平面对应的法向量，借助法向量的夹角求二面角，利用向量的夹角公式，求出异面直线所成角的余弦值，利用已知条件，求出
的值.
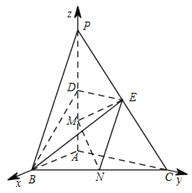
试题解析：如图，以A为原点，分别以
， 
， 
方向为x轴、y轴、z轴正方向建立空间直角坐标系.依题意可得A（0，0，0），B（2，0，0），C（0，4，0），P（0，0，4），D（0，0，2），E（0，2，2），M（0，0，1），N（1，2，0）.
（Ⅰ）证明： 
=（0，2，0），
=（2，0， 
）.设
，为平面BDE的法向量，
则
，即
.不妨设
，可得
.又
=（1，2， 
），可得
.
因为
平面BDE，所以MN//平面BDE.
（Ⅱ）解：易知
为平面CEM的一个法向量.设
为平面EMN的法向量，则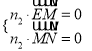
，因为
， 
，所以
.不妨设
，可得
.
因此有
，于是
.
所以，二面角C—EM—N的正弦值为
.
（Ⅲ）解：依题意，设AH=h（
），则H（0，0，h），进而可得
， 
.由已知，得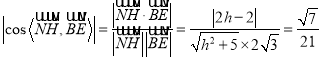
，整理得
，解得
，或
.
所以，线段AH的长为
或
.
练习册系列答案
相关题目
