题目内容
设函数f(x)=x+ax2+bln x,曲线y=f(x)在点P(1,0)处的切线斜率为2.
(1)求a,b的值;
(2)证明:f(x)≤2x-2.
(1)求a,b的值;
(2)证明:f(x)≤2x-2.
(1)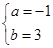 (2)见解析
(2)见解析
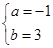 (2)见解析
(2)见解析(1)f′(x)=1+2ax+ ,
,
由题设,y=f(x)在点P(1,0)处切线的斜率为2.
∴ 解之得
解之得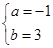
因此实数a,b的值分别为-1和3.
(2)f(x)定义域(0,+∞),且f(x)=x-x2+3ln x.
设g(x)=f(x)-(2x-2)=2-x-x2+3ln x,
则g′(x)=-1-2x+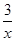 =-
=- .?
.?
当0<x<1时,g′(x)>0;当x>1时,g′(x)<0.
∴g(x)在(0,1)上单调递增;在(1,+∞)上单调减少.
∴g(x)在x=1处有最大值g(1)=0
故g(x)≤0,即f(x)≤2x-2.
 ,
,由题设,y=f(x)在点P(1,0)处切线的斜率为2.
∴
 解之得
解之得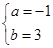
因此实数a,b的值分别为-1和3.
(2)f(x)定义域(0,+∞),且f(x)=x-x2+3ln x.
设g(x)=f(x)-(2x-2)=2-x-x2+3ln x,
则g′(x)=-1-2x+
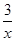 =-
=- .?
.?当0<x<1时,g′(x)>0;当x>1时,g′(x)<0.
∴g(x)在(0,1)上单调递增;在(1,+∞)上单调减少.
∴g(x)在x=1处有最大值g(1)=0
故g(x)≤0,即f(x)≤2x-2.

练习册系列答案
相关题目
 .
. 的单调区间;
的单调区间; 有解,求实数m的取值范围;
有解,求实数m的取值范围;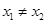 ,使
,使 成立,求证:
成立,求证: .
.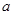 为实常数,函数
为实常数,函数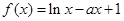 .
.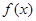 的单调性;
的单调性; ;
; 且
且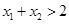 .(注:
.(注: 为自然对数的底数)
为自然对数的底数) ,(
,( 且
且 ).
).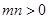 ,令
,令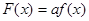 ,试判断函数
,试判断函数 在
在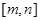 上的单调性并证明你的结论;
上的单调性并证明你的结论;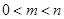 且
且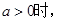
 的定义域和值域都是
的定义域和值域都是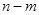 的最大值;
的最大值;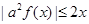 对
对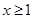 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;


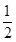 ax2-2x(a≠0)存在单调递减区间,则实数a的取值范围是______.
ax2-2x(a≠0)存在单调递减区间,则实数a的取值范围是______.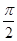 时,
时,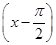 f′(x)>0.则函数y=f(x)-sin x在[-2π,2π]上的零点个数为________.
f′(x)>0.则函数y=f(x)-sin x在[-2π,2π]上的零点个数为________. x3+bx有三个单调区间,则b的取值范围是________.
x3+bx有三个单调区间,则b的取值范围是________.