题目内容
已知f(x)=(
)2(x>1),
(1)若g(x)=
+
+2,求g(x)的最小值;
(2)若不等式(1-
)•f-1(x)>m•(m-
)对于一切x∈[
,
]恒成立,求实数m的取值范围.
| x-1 |
| x+1 |
(1)若g(x)=
| 1 |
| f-1(x) |
| x |
(2)若不等式(1-
| x |
| x |
| 1 |
| 4 |
| 1 |
| 2 |
(1)f-1(x)=
(0<x<1),
∴g(x)=
+
+2=
+1+
≥2
,等号当且仅当
=1+
,即x=3-2
时取得.
∴g(x)的最小值为2
.
(2)不等式即为1+
>m(m-
),也就是(1+m)
+(1-m2)>0,
令u=
,则F(u)=(1+m)u+(1-m2)>0在[
,
]上恒成立,
∴F(
)>0且F(
)>0,解得-1<m<
.
1+
| ||
1-
|
∴g(x)=
1-
| ||
1+
|
| x |
| 2 | ||
1+
|
| x |
| 2 |
| 2 | ||
1+
|
| x |
| 2 |
∴g(x)的最小值为2
| 2 |
(2)不等式即为1+
| x |
| x |
| x |
令u=
| x |
| 1 |
| 2 |
| ||
| 2 |
∴F(
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |

练习册系列答案
相关题目
 ]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由。
]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由。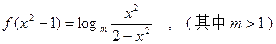
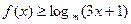
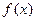 是偶函数,且当
是偶函数,且当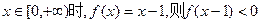 的解集是( )
的解集是( )