题目内容
当x>1时,不等式mx2+mx+1≥x恒成立,则实数m的取值范围是( )
A.[3+2
| B.(-∞,3+2
| C.[3-2
| D.(-∞,3-2
|
由不等式mx2+mx+1≥x得m(x2+x)≥x-1,又x2+x>0,所以有m≥
在(1,+∞)上恒成立,
而
=
=
=
,
∵x-1+
+3≥3+2
,当且仅当x=1+
时等号成立,即
≤
=3-2
,所以实数m的取值范围是[3-2
,+∞).
故选C.
| x-1 |
| x2+x |
而
| x-1 |
| x2+x |
| 1 | ||
|
| 1 | ||
x+
|
| 1 | ||
x-1+
|
∵x-1+
| 2 |
| x-1 |
| 2 |
| 2 |
| 1 | ||
x-1+
|
| 1 | ||
3+2
|
| 2 |
| 2 |
故选C.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
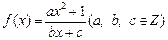 是奇函数,又,
是奇函数,又,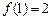 ,
,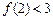 ,
,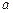 、
、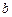 、
、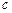 的值.
的值.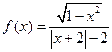 (2)
(2)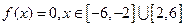
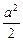 ,
,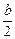 ),
),