题目内容
已知奇函数f(x)的定义域为R,且f(x)在[0,+∞)上是增函数,是否存在实数m,使f(cos2θ-3)+f(4m-2mcosθ)>f(0)对所有θ∈[0, ]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由。
]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由。
 ]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由。
]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由。符合题目要求的m的值存在,其取值范围是m>4-2 .
.
 .
. ∵f(x)是R上的奇函数,且在[0,+∞)上是增函数,∴f(x)是R上的增函数。于是不等式可等价地转化为f(cos2θ-3)>f(2mcosθ-4m),
即cos2θ-3>2mcosθ-4m,即cos2θ-mcosθ+2m-2>0。
设t=cosθ,则问题等价地转化为函数
g(t)=t2-mt+2m-2=(t-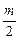 )2-
)2- +2m-2在[0,1]上的值恒为正,又转化为函数g(t)在[0,1]上的最小值为正。
+2m-2在[0,1]上的值恒为正,又转化为函数g(t)在[0,1]上的最小值为正。
∴当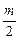 <0,即m<0时,g(0)=2m-2>0
<0,即m<0时,g(0)=2m-2>0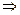 m>1与m<0不符;
m>1与m<0不符;
当0≤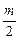 ≤1时,即0≤m≤2时,g(m)=-
≤1时,即0≤m≤2时,g(m)=- +2m-2>0
+2m-2>0
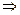 4-2
4-2 <m<4+2
<m<4+2 ,∴4-2
,∴4-2 <m≤2.
<m≤2.
当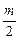 >1,即m>2时,g(1)=m-1>0
>1,即m>2时,g(1)=m-1>0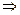 m>1
m>1 ∴m>2
∴m>2
综上,符合题目要求的m的值存在,其取值范围是m>4-2 .
.
另法(仅限当m能够解出的情况) cos2θ-mcosθ+2m-2>0对于θ∈[0,
cos2θ-mcosθ+2m-2>0对于θ∈[0, ]恒成立,
]恒成立,
等价于m>(2-cos2θ)/(2-cosθ) 对于θ∈[0, ]恒成立
]恒成立
∵当θ∈[0, ]时,(2-cos2θ)/(2-cosθ) ≤4-2
]时,(2-cos2θ)/(2-cosθ) ≤4-2 ,
,
∴m>4-2 .
.
即cos2θ-3>2mcosθ-4m,即cos2θ-mcosθ+2m-2>0。
设t=cosθ,则问题等价地转化为函数
g(t)=t2-mt+2m-2=(t-
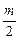 )2-
)2- +2m-2在[0,1]上的值恒为正,又转化为函数g(t)在[0,1]上的最小值为正。
+2m-2在[0,1]上的值恒为正,又转化为函数g(t)在[0,1]上的最小值为正。∴当
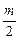 <0,即m<0时,g(0)=2m-2>0
<0,即m<0时,g(0)=2m-2>0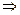 m>1与m<0不符;
m>1与m<0不符;当0≤
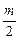 ≤1时,即0≤m≤2时,g(m)=-
≤1时,即0≤m≤2时,g(m)=- +2m-2>0
+2m-2>0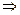 4-2
4-2 <m<4+2
<m<4+2 ,∴4-2
,∴4-2 <m≤2.
<m≤2.当
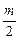 >1,即m>2时,g(1)=m-1>0
>1,即m>2时,g(1)=m-1>0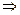 m>1
m>1 ∴m>2
∴m>2综上,符合题目要求的m的值存在,其取值范围是m>4-2
 .
.另法(仅限当m能够解出的情况)
 cos2θ-mcosθ+2m-2>0对于θ∈[0,
cos2θ-mcosθ+2m-2>0对于θ∈[0, ]恒成立,
]恒成立,等价于m>(2-cos2θ)/(2-cosθ) 对于θ∈[0,
 ]恒成立
]恒成立∵当θ∈[0,
 ]时,(2-cos2θ)/(2-cosθ) ≤4-2
]时,(2-cos2θ)/(2-cosθ) ≤4-2 ,
,∴m>4-2
 .
.
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
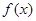 满足条件:当
满足条件:当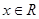 时,恒有
时,恒有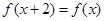 ,且
,且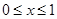 时,有
时,有 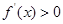 则
则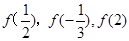 的大小关系为 ( )
的大小关系为 ( )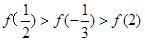
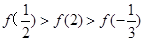

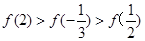
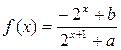
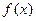 的解析式;
的解析式;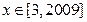 ,不等式
,不等式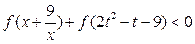 恒成立,求t
恒成立,求t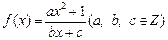 是奇函数,又,
是奇函数,又,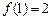 ,
,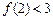 ,
,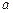 、
、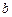 、
、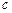 的值.
的值.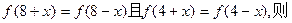
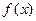 是( )
是( )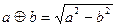 ,
, ,则
,则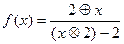
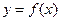 为奇函数,若
为奇函数,若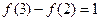 ,则
,则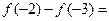 .
.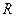 上的奇函数
上的奇函数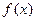 ,当
,当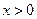 时,
时,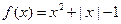 ,那么
,那么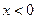 时,
时,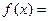 .
.