题目内容
对于任意满足θ∈[0,
]的θ,使得|sinθ-pcosθ-q|≤
恒成立的所有实数对(p,q)是______.
| π |
| 2 |
| ||
| 2 |
∵对于任意满足θ∈[0,
]的θ,使得|sinθ-pcosθ-q|≤
恒成立
∴当θ=0时,|p+q|≤
①
当θ=
时,|
(1-p)-q|≤
②
当θ=
时,|1-q|≤
③
①+②-1-2
≤p≤-1
由②③消去q得-1≤p≤3-2
∴p=-1
∴|
sin(θ+
)-q|≤
∴|
-q|≤
,|1-q|≤
解得q=
∴实数对(p,q)是(-1,
)
故答案为:(-1,
)
| π |
| 2 |
| ||
| 2 |
∴当θ=0时,|p+q|≤
| ||
| 2 |
当θ=
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
当θ=
| π |
| 2 |
| ||
| 2 |
①+②-1-2
| 2 |
由②③消去q得-1≤p≤3-2
| 2 |
∴p=-1
∴|
| 2 |
| π |
| 4 |
| ||
| 2 |
∴|
| 2 |
| ||
| 2 |
| ||
| 2 |
解得q=
1+
| ||
| 2 |
∴实数对(p,q)是(-1,
1+
| ||
| 2 |
故答案为:(-1,
1+
| ||
| 2 |

练习册系列答案
相关题目
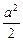 ,
,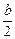 ),
),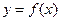 为奇函数,若
为奇函数,若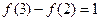 ,则
,则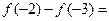 .
.