题目内容
已知函数f(x)=
,满足对任意的x1≠x2都有
<0成立,则a的取值范围是( )
|
| f(x1)-f(x2) |
| x1-x2 |
A.(0,
| B.(0,1) | C.[
| D.(0,3) |
∵f(x)对任意的x1≠x2都有
<0成立,
∴f(x)=
为R上的减函数,
∴
解得0<a≤
.
故选A.
| f(x1)-f(x2) |
| x1-x2 |
∴f(x)=
|
∴
|
| 1 |
| 4 |
故选A.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
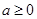 ,函数
,函数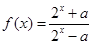
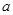 =4,求函数
=4,求函数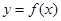 的反函数
的反函数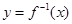 ;
;
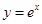 的图象与
的图象与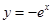 的图象关于
的图象关于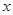 轴对称;
轴对称;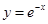 的图象关于
的图象关于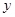 轴对称;
轴对称;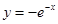 的图象关于坐标原点对称.
的图象关于坐标原点对称.