题目内容
(本题满分14分)本题有2个小题,第一小题满分6分,第二小题满分1分.
设常数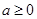 ,函数
,函数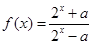
(1)若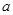 =4,求函数
=4,求函数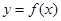 的反函数
的反函数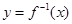 ;
;
(2)根据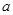 的不同取值,讨论函数
的不同取值,讨论函数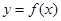 的奇偶性,并说明理由.
的奇偶性,并说明理由.
设常数
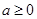 ,函数
,函数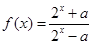
(1)若
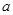 =4,求函数
=4,求函数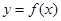 的反函数
的反函数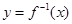 ;
;(2)根据
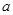 的不同取值,讨论函数
的不同取值,讨论函数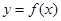 的奇偶性,并说明理由.
的奇偶性,并说明理由.(1)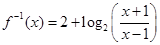 ,
,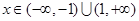 ;(2)
;(2)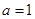 时
时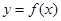 为奇函数,当
为奇函数,当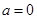 时
时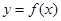 为偶函数,当
为偶函数,当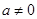 且
且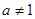 时
时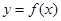 为非奇非偶函数.
为非奇非偶函数.
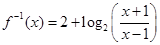 ,
,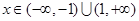 ;(2)
;(2)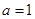 时
时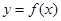 为奇函数,当
为奇函数,当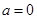 时
时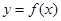 为偶函数,当
为偶函数,当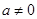 且
且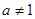 时
时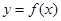 为非奇非偶函数.
为非奇非偶函数.试题分析:(1)求反函数,就是把函数式
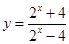 作为关于
作为关于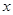 的方程,解出
的方程,解出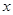 ,得
,得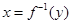 ,再把此式中的
,再把此式中的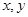 互换,即得反函数的解析式,还要注意的是一般要求出原函数的值域,即为反函数的定义域;(2)讨论函数的奇偶性,我们可以根据奇偶性的定义求解,在
互换,即得反函数的解析式,还要注意的是一般要求出原函数的值域,即为反函数的定义域;(2)讨论函数的奇偶性,我们可以根据奇偶性的定义求解,在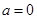 ,
,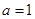 这两种情况下,由奇偶性的定义可知函数
这两种情况下,由奇偶性的定义可知函数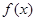 具有奇偶性,在
具有奇偶性,在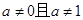 时,函数的定义域是
时,函数的定义域是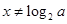 ,不关于原点对称,因此函数既不是奇函数也不是偶函数.
,不关于原点对称,因此函数既不是奇函数也不是偶函数.试题解析:(1)由
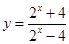 ,解得
,解得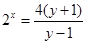 ,从而
,从而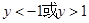 ,
,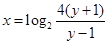
∴
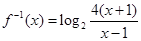 ,
,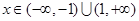
∵
 且
且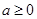
∴①当
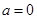 时,
时,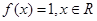 ,
,∴对任意的
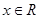 都有
都有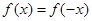 ,∴
,∴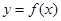 为偶函数
为偶函数②当
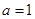 时,
时,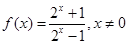 ,
,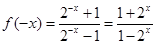 ,
,∴对任意的
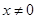 且
且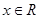 都有
都有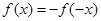 ,∴
,∴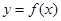 为奇函数
为奇函数③当
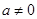 且
且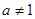 时,定义域为
时,定义域为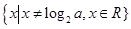 ,
,∴定义域不关于原定对称,∴
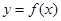 为非奇非偶函数
为非奇非偶函数【考点】反函数,函数奇偶性.

练习册系列答案
相关题目
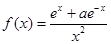 是奇函数,则实数
是奇函数,则实数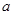 的值为 .
的值为 .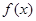 是定义在
是定义在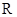 上的奇函数,当
上的奇函数,当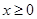 时,
时,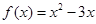 ,则函数
,则函数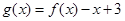 的零点的集合为( )
的零点的集合为( )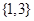
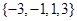
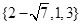
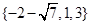
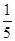 ,则f(log220)的值为( )
,则f(log220)的值为( )
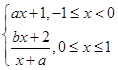 ,其中a,b∈R.若f
,其中a,b∈R.若f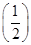 =f
=f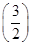 ,则a+3b的值为________.
,则a+3b的值为________.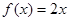 ,
,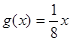 ,若
,若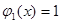 ,对
,对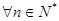 ,
,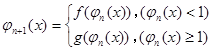 ,则
,则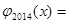 。
。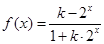 在定义域上为奇函数,则实数
在定义域上为奇函数,则实数 .
.