题目内容
17.若全集U={x∈R|x2≤4},A={x∈R|-2≤x≤0},则∁UA=( )| A. | (0,2) | B. | [0,2) | C. | (0,2] | D. | [0,2] |
分析 解二次不等式求出集合U,进而根据集合补集运算的定义,可得答案.
解答 解:∵全集U={x∈R|x2≤4}=[-2,2],
A={x∈R|-2≤x≤0}=[-2,0],
则∁UA=(0,2],
故选:C
点评 本题考查的知识点是集合的交集,并集,补集运算,熟练掌握并正确理解集合运算的定义是解答的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
12.已知函数f(x)=aln(x+1)-x2在区间(1,2)内任取两个实数p,q,且p≠q,不等式$\frac{{f({p+1})-f({q+1})}}{p-q}<1$恒成立,则实数a的取值范围为( )
| A. | a≤15 | B. | 0<a≤15 | C. | a>6 | D. | a<-3 |
9.已知集合A={x||x-$\frac{1}{2}$|≤$\frac{3}{2}$},B={x|y=lg(4x-x2)},则A∩B等于( )
| A. | (0,2] | B. | [-1,0) | C. | [2,4) | D. | [1,4) |
6.如图所示,当输入的实数x∈[2,30]时,执行如图所示的程序框图,则输出的x不小于111的概率是( )


| A. | $\frac{8}{13}$ | B. | $\frac{17}{28}$ | C. | $\frac{2}{3}$ | D. | $\frac{18}{29}$ |
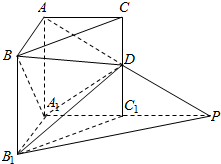 如图所示,在直三棱柱ABC-A1B1B1中,∠BAC=90°,AB=AC=AA1=1,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1.
如图所示,在直三棱柱ABC-A1B1B1中,∠BAC=90°,AB=AC=AA1=1,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1.