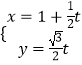Question

【题目】设命题p：函数y=sin2x的最小正周期为 ；命题q：函数y=cosx的图象关于直线x= 对称．则下列判断正确的是（ ）
A.p为真
B.￢q为假
C.p∧q为假
D.p∨q为真

Answer 1

【答案】C
【解析】解：由于函数y=sin2x的最小正周期为π，故命题p是假命题；函数y=cosx的图象关于直线x=kπ对称，k∈Z，故q是假命题．结合复合命题的判断规则知：￢q为真命题，p∧q为假命题，p∨q为是假命题．

故选C．

【考点精析】本题主要考查了复合命题的真假和余弦函数的对称性的相关知识点，需要掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反；“p且q”形式复合命题当P与q同为真时为真，其他情况时为假；“p或q”形式复合命题当p与q同为假时为假，其他情况时为真；余弦函数的对称性：对称中心；对称轴才能正确解答此题．