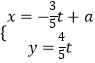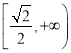题目内容
【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程![]()
![]() 关于时间
关于时间![]() 的函数关系式分别为
的函数关系式分别为![]() ,
,![]() ,
,![]() ,
,![]() ,有以下结论:
,有以下结论:
①当![]() 时,甲走在最前面;
时,甲走在最前面;
②当![]() 时,乙走在最前面;
时,乙走在最前面;
③当![]() 时,丁走在最前面,当
时,丁走在最前面,当![]() 时,丁走在最后面;
时,丁走在最后面;
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为 (把正确结论的序号都填上,多填或少填均不得分).
【答案】③④⑤
【解析】路程![]() 关于时间
关于时间![]() 的函数关系式是
的函数关系式是![]() ,
,![]() ,
,![]() ,
,![]() ,
,
它们相应的函数模型分别是指数型函数,二次函数,一次函数,和对数型函数模型.
当![]() 时,
时,![]() ,∴命题①不正确;
,∴命题①不正确;
当![]() 时,
时,![]() ,∴命题②不正确;
,∴命题②不正确;
对数型函数的变化是先快后慢,当![]() 时,甲、乙、丙、丁四个物体重合,从而可知当
时,甲、乙、丙、丁四个物体重合,从而可知当![]() 时,丁走在最前面,当
时,丁走在最前面,当![]() 时,丁走在最后面,命题③正确;
时,丁走在最后面,命题③正确;
指数型函数变化是先慢后快,当运动的时间足够长时,最前面的物体一定是按照指数型函数运动的物体,即一定是甲物体,∴命题⑤正确.
结合对数型和指数型函数的图象变化情况,可知丙不可能走在最前面,也不可能走在最后面,命题④正确.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=![]() a,
a,
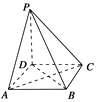
(1)求证:PD⊥平面ABCD;
(2)求证:平面PAC⊥平面PBD;
(3)求二面角P-AC-D的正切值.
【题目】某企业想通过做广告来提高销售额,经预测可知本企业产品的广告费x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
由表中的数据得线性回归方程为 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =6.5,由此预测当广告费为7百万元时,销售额为万元.
=6.5,由此预测当广告费为7百万元时,销售额为万元.