题目内容
【题目】在直角坐标系xOy中，直线C1的参数方程为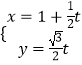 
（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ2（1+2sin2θ）=3．
（Ⅰ）写出C1的普通方程和C2的直角坐标方程；
（Ⅱ）直线C1与曲线C2相交于A，B两点，点M（1，0），求||MA|﹣|MB||．
【答案】解：（Ⅰ）∵直线C1的参数方程为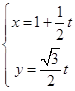 
（t为参数），
∴消去参数，得：曲线C1的普通方程为 
，
∵曲线C2的极坐标方程为ρ2（1+2sin2θ）=3，
ρ2=x2+y2，ρsinθ=y，
∴曲线C2的直角坐标方程为 
．
（Ⅱ）将直线C1的参数方程代入C2的直角坐标方程，
整理得：5t2+2t﹣4=0， 
，
由t的几何意义可知： 
【解析】（Ⅰ）直线C1的参数方程消去参数，能求出曲线C1的普通方程；曲线C2的极坐标方程中，由ρ2=x2+y2，ρsinθ=y，能求出曲线C2的直角坐标方程．（Ⅱ）将直线C1的参数方程代入C2的直角坐标方程，整理得：5t2+2t﹣4=0，由t的几何意义能求出||MA|﹣|MB||．
练习册系列答案
相关题目
【题目】某企业想通过做广告来提高销售额，经预测可知本企业产品的广告费x（单位：百万元）与销售额y（单位：百万元）之间有如下对应数据：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
由表中的数据得线性回归方程为 
= 
x+ 
，其中 =6.5，由此预测当广告费为7百万元时，销售额为万元．
