题目内容
【题目】已知右焦点为F(c,0)的椭圆M: ![]() =1(a>b>0)过点
=1(a>b>0)过点 ![]() ,且椭圆M关于直线x=c对称的图形过坐标原点.
,且椭圆M关于直线x=c对称的图形过坐标原点.
(1)求椭圆M的方程;
(2)过点(4,0)且不垂直于y轴的直线与椭圆M交于P,Q两点,点Q关于x轴的对称原点为E,证明:直线PE与x轴的交点为F.
【答案】
(1)解:由题意可知:椭圆M: ![]() =1(a>b>0)焦点在x轴上,
=1(a>b>0)焦点在x轴上,
椭圆过点 ![]() ,即
,即 ![]() ,
,
椭圆M关于直线x=c对称的图形过坐标原点,
∴a=2c,
由a2=b2+c2,则b2= ![]() a2,
a2,
解得:a2=4,b2=3,
∴椭圆的标准方程 ![]()
(2)证明:设直线PQ的方程为:y=k(x﹣4),k≠0,
∴ 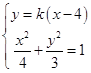 ,整理得:(3+4k2)x2﹣32k2x+64k2﹣12=0,
,整理得:(3+4k2)x2﹣32k2x+64k2﹣12=0,
∵过点P0(4,0)且不垂直于x轴的直线与椭圆交于P,Q两点,
∴由△=(﹣32k2)2﹣4(3+4k2)(64k2﹣12)>0,得:k∈(﹣ ![]() ,
, ![]() ),
),
设P(x1,y1),Q(x2,y2),E(x4,﹣y4),
则x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
则直线AE的方程为y﹣y1= ![]() (x﹣x1),
(x﹣x1),
令y=0得:x=﹣y1 ![]() +x1=
+x1= ![]() =
= ![]() =
= ![]() =
= 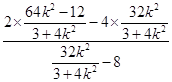 =1.
=1.
∴直线PE过定点(1,0),
由椭圆的焦点坐标为(1,0),则直线PE与x轴的交点为F.
【解析】(1)由题意可知:椭圆M: ![]() =1(a>b>0)焦点在x轴上,将点
=1(a>b>0)焦点在x轴上,将点 ![]() 代入椭圆上,即
代入椭圆上,即 ![]() ,a=2c,则b2=
,a=2c,则b2= ![]() a2,即可求得a和b的值,求得椭圆方程;(2)设直线PQ的方程为:y=k(x﹣4),k≠0,代入椭圆方程,得(3+4k2)x2﹣32k2x+64k2﹣12=0,由根的判别式得到k∈(﹣
a2,即可求得a和b的值,求得椭圆方程;(2)设直线PQ的方程为:y=k(x﹣4),k≠0,代入椭圆方程,得(3+4k2)x2﹣32k2x+64k2﹣12=0,由根的判别式得到k∈(﹣ ![]() ,
, ![]() ),由韦达定理及直线的方程代入x=﹣y1
),由韦达定理及直线的方程代入x=﹣y1 ![]() +x1=1,由此能证明直线AE过定点(1,0),由椭圆的焦点坐标为(1,0),则直线PE与x轴的交点为F.
+x1=1,由此能证明直线AE过定点(1,0),由椭圆的焦点坐标为(1,0),则直线PE与x轴的交点为F.