题目内容
20.若a、b、c∈R,a>b,则下列不等式成立的是( )| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | a2>b2 | C. | $\frac{a}{{c}^{2}+1}$>$\frac{b}{{c}^{2}+1}$ | D. | |a|>|b| |
分析 A.取a=1,b=-2,即可判断出正误;
B.取a=1,b=-2,即可判断出正误;
C.由于a>b,c2+1>0,利用不等式的基本性质可得$\frac{a}{{c}^{2}+1}>$$\frac{b}{{c}^{2}+1}$;
D.取a=1,b=-2,即可判断出正误.
解答 解:A.取a=1,b=-2,则$\frac{1}{a}$<$\frac{1}{b}$不成立;
B.取a=1,b=-2,则a2>b2不成立;
C.∵a>b,c2+1>0,∴$\frac{a}{{c}^{2}+1}>$$\frac{b}{{c}^{2}+1}$,成立.
D.取a=1,b=-2,则|a|>|b|不成立.
故选:C.
点评 本题考查了不等式的基本性质、举反例否定一个命题,考查了推理能力,属于基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
10.已知数列{an}的首项为a1=1,且满足对任意的n∈N*,都有an+1-an=2n成立,则a2015=( )
| A. | 22014-1 | B. | 22015-1 | C. | 22015+1 | D. | 22016-1 |
5.当-1<m<1时,复数z=$\frac{-1+i}{m+i}$(i为虚数单位)在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
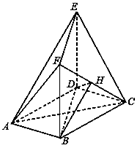 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.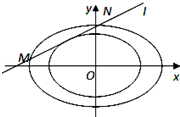 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,点M在椭圆C上,点M到椭圆C的两个焦点的距离之和是4.
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,点M在椭圆C上,点M到椭圆C的两个焦点的距离之和是4.