题目内容
10.已知数列{an}的首项为a1=1,且满足对任意的n∈N*,都有an+1-an=2n成立,则a2015=( )| A. | 22014-1 | B. | 22015-1 | C. | 22015+1 | D. | 22016-1 |
分析 已知递推关系an-an-1=2n-1,累加计算即可.
解答 解:∵an+1-an=2n,
∴an-an-1=2n-1,
an-1-an-2=2n-2,
…
a2-a1=21,
累加得:an=2n-1+2n-2+2n-3+…+2+1=2n-1,
∴${a_{2015}}={2^{2015}}-1$,
故选:B.
点评 本题考查求数列的通项,利用累加法是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
1.已知数列{an}的通项公式为${a_n}={2^{5-n}}$,数列{bn}的通项公式为bn=n+k,设${c_n}=\left\{\begin{array}{l}{b_n},{a_n}≤{b_n}\\{a_n},{a_n}>{b_n}\end{array}\right.$,若在数列{cn}中,c5≤cn对任意n∈N*恒成立,则实数k的取值范围是( )
| A. | -5≤k≤-4 | B. | -4≤k≤-3 | C. | -5≤k≤-3 | D. | k=-4 |
5.已知函数f(x)=x2-cosx,则$f(\frac{3}{5}),f(0),f(-\frac{1}{2})$的大小关系是( )
| A. | $f(0)<f(\frac{3}{5})<f(-\frac{1}{2})$ | B. | $f(0)<f(-\frac{1}{2})<f(\frac{3}{5})$ | C. | $f(\frac{3}{5})<f(-\frac{1}{2})<f(0)$ | D. | $f(-\frac{1}{2})<f(0)<f(\frac{3}{5})$ |
2.设i为虚数单位,则|1-i|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
20.若a、b、c∈R,a>b,则下列不等式成立的是( )
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | a2>b2 | C. | $\frac{a}{{c}^{2}+1}$>$\frac{b}{{c}^{2}+1}$ | D. | |a|>|b| |
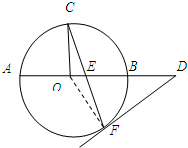 如图,AB是⊙O的直径,C,F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连结CF交AB于点E,OA=3,DB=3,则DE=3$\sqrt{3}$.
如图,AB是⊙O的直径,C,F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连结CF交AB于点E,OA=3,DB=3,则DE=3$\sqrt{3}$.