题目内容
12.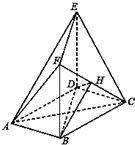 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.(1)求证:AC⊥平面BDEF;
(2)求二面角H-BD-C的大小.
分析 (1)由面面垂直的性质可证AC与平面BDEF垂直;
(2)以O为原点,OB,OC,ON所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,求出平面BDH、平面BCD的法向量,利用向量的夹角公式,即可求二面角H-BD-C的大小.
解答 (1)证明:∵四边形ABCD是菱形,
∴AC⊥BD.
又∵平面BDEF⊥平面ABCD,平面BDEF∩平面ABCD=BD,
且AC?平面ABCD,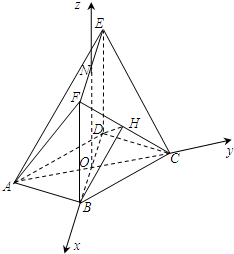
∴AC⊥平面BDEF;
(2)解:设AC∩BD=O,取EF的中点N,连接ON,
∵四边形BDEF是矩形,O,N分别为BD,EF的中点,
∴ON∥ED,
∵ED⊥平面ABCD,
∴ON⊥平面ABCD,
由AC⊥BD,得OB,OC,ON两两垂直.
∴以O为原点,OB,OC,ON所在直线分别为x轴,y轴,z轴,如图建立空间直角坐标系.
∵底面ABCD是边长为2的菱形,∠BAD=60°,BF=3,
∴B(1,0,0),D(-1,0,0),H($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$)
∴$\overrightarrow{BH}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$),$\overrightarrow{DB}$=(2,0,0).
设平面BDH的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{-x+\sqrt{3}y+3z=0}\\{2x=0}\end{array}\right.$
令z=1,得$\overrightarrow{n}$=(0,-$\sqrt{3}$,1)
由ED⊥平面ABCD,得平面BCD的法向量为$\overrightarrow{ED}$=(0,0,-3),
则cos<$\overrightarrow{ED}$,$\overrightarrow{n}$>=-$\frac{1}{2}$,
由图可知二面角H-BD-C为锐角,
∴二面角H-BD-C的大小为60°
点评 本题考查面面垂直的性质,考查线面垂直,考查面面角,考查向量法的运用,正确求出平面的法向量是关键.

 阅读快车系列答案
阅读快车系列答案| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
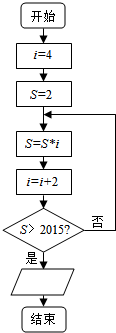
| A. | 输出i-2 | B. | 输出i-1 | C. | 输出i | D. | 输出i+1 |
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | a2>b2 | C. | $\frac{a}{{c}^{2}+1}$>$\frac{b}{{c}^{2}+1}$ | D. | |a|>|b| |
| A. | 1 | B. | 2 | C. | 4 | D. | 无法确定 |
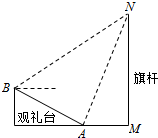 2014年足球世界杯赛上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和45°,若旗杆的高度为30米,则且座位A、B的距离为10($\sqrt{6}$-$\sqrt{2}$) 米.
2014年足球世界杯赛上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和45°,若旗杆的高度为30米,则且座位A、B的距离为10($\sqrt{6}$-$\sqrt{2}$) 米.